DM math
54 messages
- Page 2 sur 3 - 1, 2, 3
Re: DM math
l'objet de ce DM est de montrer que le système "somme-produit" d'inconnues (u,v) est équivalent à la résolution d'une équation du second degré à coefficients bien choisis.
Et tu connais une condition nécessaire et suffisante (CNS) sur les coefficients d'une équation du second degré pour qu'elle admette des solutions réelles (le discriminant a été inventé pour ça)
Et tu connais une condition nécessaire et suffisante (CNS) sur les coefficients d'une équation du second degré pour qu'elle admette des solutions réelles (le discriminant a été inventé pour ça)
Re: DM math
Bonjour et merci pour l'aide
Désolé, mais je ne comprends pas : une condition nécessaire et suffisante sur les coefficients d'une équation de second degré pour qu'elle admette des racines réelles.
d'après mon cours tout ce que je comprends , c'est ça :
si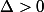
alors il y a deux racines
si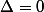
alors présence d'une racine double
si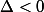
pas de racine
Désolé, mais je ne comprends pas : une condition nécessaire et suffisante sur les coefficients d'une équation de second degré pour qu'elle admette des racines réelles.
d'après mon cours tout ce que je comprends , c'est ça :
si
alors il y a deux racines
si
alors présence d'une racine double
si
pas de racine
Re: DM math
donc l'équation ax^2+bx+c=0 admet des racines réelles (éventuellement double) si et seulement si ....
Re: DM math
alors :
soit :
et j'ai une fonction affine, c'est à dire une droite donc pas de racines
-
Re: DM math
Bonjour,
soit l'équation du second degré ax²+bx+c=0 qui admet pour racines u et v.
Après avoir calculé delta, comment exprimes-tu u et v en fonction de a, b et delta ?
Tu peux ensuite calculer S=u+v et P=u.v en fonction de a, b et c.
soit l'équation du second degré ax²+bx+c=0 qui admet pour racines u et v.
Après avoir calculé delta, comment exprimes-tu u et v en fonction de a, b et delta ?
Tu peux ensuite calculer S=u+v et P=u.v en fonction de a, b et c.
Re: DM math
je pars de :
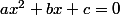
mise en facteur de et j'arrive à :
et j'arrive à :
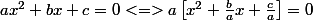
Je factorise :
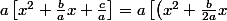^2 - \left(\frac{b}{2a}\right)^2 + \frac{c}{a}\right] = 0)
^2 - \left(\frac{b}{2a}\right)^2\right + \frac{c}{a} ] = a \left[\left(x + \frac{b}{2a}\right)^2 - \frac{b^2}{4a^2} + \frac{c}{a}\right])
Les 2 fractions en dehors des parenthèses ont le même dénominateur , je peux les additionner
^2 - \left( \frac{b}{2a}\right)^2\ + \frac{c}{a}\right] = a \left[\left(x + \frac{b}{2a}\right)^2 - \frac{b^2}{4a^2} + \frac{4ac}{4a^2}\right] = 0)
j'arrive à :
^2 - \left( \frac{b}{2a}\right)^2 + \frac{c}{a}\right ] = a \left[\left(x + \frac{b}{2a}\right)^2 + \frac{-b^2 + 4ac}{4a^2}\right] = 0)
maintenant je peux factoriser l'expression que si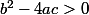
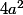 est lui toujours positif puisque un carré est toujours positif
est lui toujours positif puisque un carré est toujours positif
donc si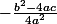
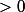 je factorise et j'arrive à :
je factorise et j'arrive à :
 \times \left(x + \frac{b}{2a} + \sqrt{ \frac{b^2 - 4ac}{4a^2}}\right) = 0)
 \times \left(x + \frac{b}{2a} - \sqrt{ \frac{b^2 - 4ac}{4a^2}}\right) = a \left(x + \frac{b}{2a} + \frac{\sqrt{b^2 - 4ac}}{\sqrt{4a^2}} \right)\times \left(x + \frac{b}{2a} - \frac{\sqrt{b^2 - 4ac}}{\sqrt{4a^2}}\right) = 0)
 \times \left(x + \frac{b}{2a} - \frac{\sqrt{b^2 - 4ac}}{\sqrt{4a^2}} \right) = a\left(x + \frac{b}{2a} + \frac{\sqrt{b - 4ac}}{2a}\right) \times \left(x + \frac{b}{2a} - \frac{\sqrt{b - 4ac}}{2a}\right) = 0)
 = 0) ou bien
ou bien  = 0)
1 er cas :
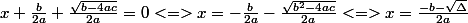
2 e cas :
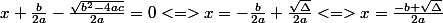
-
mise en facteur de
Je factorise :
Les 2 fractions en dehors des parenthèses ont le même dénominateur , je peux les additionner
j'arrive à :
maintenant je peux factoriser l'expression que si
donc si
1 er cas :
2 e cas :
-
Re: DM math
Très bien, tu as redémontré les formules du cours.
Ensuite, appelle la première solution u et la deuxième solution v.
Un calcul donne S=u+v=...
et P=uv=...
Ensuite, appelle la première solution u et la deuxième solution v.
Un calcul donne S=u+v=...
et P=uv=...
Re: DM math
Bonsoir et merci
Oui, j'ai re-démontré les formules du cours et je l'ai fait sans regarder le cours
Etes-vous sur qu'il n'y a pas d'erreurs dans les équivalents que j'ai écrites ?
Oui, j'ai re-démontré les formules du cours et je l'ai fait sans regarder le cours
Etes-vous sur qu'il n'y a pas d'erreurs dans les équivalents que j'ai écrites ?
Re: DM math
u + v
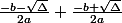
les fractions ont le même dénominateur, j'additionne les numérateurs
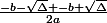
je peux simplifier les racines de delta
soit :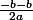
me donne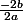
que je peux simplifier ( les 2 s'en vont )
ce qui me donne -b/a
u + v = - b/a
les fractions ont le même dénominateur, j'additionne les numérateurs
je peux simplifier les racines de delta
soit :
me donne
que je peux simplifier ( les 2 s'en vont )
ce qui me donne -b/a
u + v = - b/a
Re: DM math
je dois obtenir c/a
il y a la lettre 'c' dans l'expression de
-
Re: DM math
multiplication de deux fractions
donc je multiplie les numérateurs et les dénominateurs
mon u c'est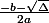
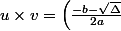 \times \left(\frac{- b +\sqrt{\Delta}}{2a}\right))
-
donc je multiplie les numérateurs et les dénominateurs
mon u c'est
-
Re: DM math
galereenpremièreS a écrit:multiplication de deux fractions
donc je multiplie les numérateurs et les dénominateurs
mon u c'est
-
Salut,
C'est bien égal à
Modifié en dernier par laetidom le 13 Oct 2018, 11:49, modifié 1 fois.
Re: DM math
donc j'ai une multiplication de deux fractions
par conséquent je multiplie les dénominateurs et les numérateurs
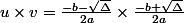
 \times \left(- b + b^2 - 4ac\right)}{2a \times 2a})
double distributivité pour le numérateur
(-b) fois (-b) me donne b carré
(-b) fois racine carré b au carré moins 4 ac me donne \times \sqrt{( b^2 - 4ac)})
- racine carrée b carré moins 4 ac fois (-b) me donne}\times (-b))
-
par conséquent je multiplie les dénominateurs et les numérateurs
double distributivité pour le numérateur
(-b) fois (-b) me donne b carré
(-b) fois racine carré b au carré moins 4 ac me donne
- racine carrée b carré moins 4 ac fois (-b) me donne
-
Re: DM math
galereenpremièreS a écrit:donc j'ai une multiplication de deux fractions
par conséquent je multiplie les dénominateurs et les numérateurs
double distributivité (donc quatre termes et non trois) pour le numérateur :
1)(-b) fois (-b) me donne b carré ok
2)(-b) fois racine carré b au carré moins 4 ac me donneok
3)- racine carrée b carré moins 4 ac fois (-b) me donneok
plus 4)x
= . . . ?
-
remarque :
2) et 3) s'annulent…,
reste alors 1) + 4)
et au dénominateur on a
Re: DM math
Il faut reconnaitre une identité remarquable du type (A-B)*(A+B)=A^2-B^2 pour simplifier le calcul et on trouve bien +c/a
54 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
