Trinôme second degré

[Snowely]

Bonjour j'ai la question suivante pour un DM, et je ne sais pas comment m'y prendre :
"Soient x1 et x2 les racines du trinôme x--> ax^2 + bx + c. Calculer x1^2 et x2^2 en fonction de a, b et c."
J'ai pensé à utiliser delta, mais je ne dépasse pas la formule b^2-4ac.
J'ai donc cherché du cours pur de 1ère S, pour trouver une démonstration semblable mais je n'ai pas trouvé. Donc si vous avez une idée, je veux bien, merci de votre aide

[Sake]

Salut,

Il faut chercher à isoler x dans ces expressions...
Si x est solution réelle de ax²+bx+c = 0, alors remarque qu'on peut réduire l'expression ax²+bx+c en écrivant sa forme canonique. Tu chercheras ensuite à mettre les constantes d'un côté de l'égalité, les termes avec x de l'autre, puis simplifier.

[Kolis]

Bonjour !
d'où ....
Tu dois évidemment imposer une condition à tes coefficients !

[Snowely]

J'ai fait la forme canonique du trinôme, j'arrive à "a(x+(b/2a))^2 -(b^2-4ac/4a^2)=0, où l'on reconnait delta. J'ai continué, et j'arrive à un point où l'équation ne semble pas avoir de fin.. "x^2+x=-b+delta/4a^2"

[Ben314]

Salut,
Je comprend pas franchement quel est l'intérêt de l'énoncé : vu que tu parle de Delta=..., je soupsonne que tu sait que et que ce qui signifie que et que . Et ça répond parfaitement à la question "exprimer et en fonction de ".
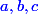Si tu as rien d'autre à faire, tu peut éventuellement développer les carrés, mais rien dans la question posé ne le demande.

[Snowely]

C'est ce que je voulais répondre au début, mais étant donné que les racines sont différentes en fonction de delta positif, négatif ou nul, est ce que l'on peut vraiment donné cette expression de x1 et x2 ?

[Ben314]

C'est ce que je voulais répondre au début, mais étant donné que les racines sont différentes en fonction de delta positif, négatif ou nul, est ce que l'on peut vraiment donné cette expression de x1 et x2 ?

Cette expression, elle est valable lorsque voire même lorsque et effectivement, si tu as vu les nombre complexes et les racines complexes d'un trinôme, alors les formules sont légèrement différentes dans le cas où .

Mais bon, c'est surtout le principe de l'exercice que je comprend pas : si tu sait exprimer les racines x1 et x2 en fonction de a,b et c, alors évidement que tu sait exprimer les carrés de ces racines en fonction de a,b et c et c'est complètement con comme question.

[Sake]

Je pensais justement que le but de l'exo était de retrouver les formules du dessus en utilisant la forme canonique

[Ben314]

Je pensais justement que le but de l'exo était de retrouver les formules du dessus en utilisant la forme canonique

Sur le principe, je dit pas que c'est pas possible, mais j'ai beau me gratter (fort) les neurones, je vois pas comment procéder pour que ce soit "plus simple" d'exprimer en fonction de plutôt que d'exprimer directement en fonction de .

Perso, le truc qui me semble relativement plausible, c'est plutôt une faute de frappe (ou de recopie) dans l'énoncé qui, pour que ce soit intéressant, pourrait demander d'exprimer en fonction de ou n'importe quoi d'autre qui soit une fonction symétrique en les deux racines et : là, il y a des méthodes astucieuses permettant d'obtenir le résultat sans passer par l'écriture des deux racines en fonction de (et ça devient un exercice classique une fois qu'on a vu les lien racines/coeff.)

[Sake]

Non je suis d'accord avec toi, il y a un petit malentendu. Mais ce que je pensais être le but de l'exo c'est de trouver de proche en proche que x_i = (-b +/- ...)/2a en effectuant le dvpt suivant :
Si x est une solution réelle de ax² + bx + c = 0, alors x satisfait à ax² + bx + c = a(x + b/(2a))² + (4ac - b²)/(4a) = ... = 0
Peut-être que j'ai mal lu, mais tu suggérais qu'il s'agissait d'une formule qui devrait être classique et connue. S'il s'avère que notre ami lycéen est en seconde ou en début de première, il fait sens de poser cet exo pour introduire le discriminant, etc.

[Ben314]

Si x est une solution réelle de ax² + bx + c = 0, alors x satisfait à ax² + bx + c = a(x + b/(2a))² + (4ac - b²)/(4a) = ... = 0

Certes, sauf que je le redit : que ce soit en partant de l'équation en rouge ou de celle en bleue, je ne vois absolument pas comment se démerder pour qu'il soit plus naturel ou plus rapide d'exprimer en fonction de que d'exprimer directement en fonction de . La forme canonique, elle permet effectivement d'exprimer (x+b/(2a))^2 [en fonction de a,b,c], sauf que, partant de (x+k)^2=quelque_chose, je ne vois absolument aucune astuce pour en déduire que x^2=quelque_chose sans passer par l'étape intermédiaire x=quelque_chose.

Bref, tout ça pour dire que si je tombais sur le forum sur un thread d'un élève qui ne connaît pas les formules Delta=... et qui aimerais les trouver par lui même, y'a un truc de sûr et certain, c'est que je lui donnerais pas comme "indication" de commencer par chercher combien vaut x^2 plutôt que x (et que si quelqu'un mettait une telle indication, je pense que je lui demanderais en M.P. où il veut en venir avec son "indication")

[Sake]

Bien-sûr, je suis d'accord avec toi. Je ne pense pas avoir suggéré de calculer x² directement, mais de trouver d'abord x (en factorisant et en isolant x dans l'égalité) puis élever au carré.