Théorème de Taylor-Lagrange

[Georges10]

Bonjour à tous,

Je ne comprend pas quelque chose sur le reste d'ordre n dans la formule de Taylor-Lagrange.
Il est dit que:

Si la fonction f (à valeurs réelles ou complexes ou même dans un espace normé) est dérivable en a jusqu'à l'ordre n ≥1 , alors la fonction R_n(x) est négligeable devant (x-a)^n .

Je veux savoir l'expression de de R_n ( x ),
Parce que dans mon cours je vois l'apparition de theta qui est compris entre 0 et 1.

Merci d'avance !

[Mimosa]

Bonjour
Oui, il existe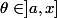 tel que . C'est une application du théorème de Rolle.

Il y a aussi une formule avec reste intégral:

[Georges10]

Bonjour
Oui, il existe tel que . C'est une application du théorème de Rolle

Considérons cette formule, on dit que R_n(x) est négligeable devant ( x-a) car
Lim ( R_n(x)/( x-a)) lorsque x tend vers a = 0
N'est ce pas ?
Donc c'est pourquoi R_n(x) est toujours substitué par o ((x-a)^n) ?

[Georges10]

Mais ce que je ne comprend pas, c'est pourquoi est ce que dans mon cours
R_n(x)= (( x-a )^n+1)f^(n+1)( a + theta ( x-a )) avec 0 < theta < 1

Je ne sais pas s'il y'a eu des transformations

Merci

[Mimosa]

est négligeable devant , on dit que c'est un .

Prendre comme dans ton cours, ou comme je l'ai écrit est équivalent. Essaye de comprendre pourquoi.

[Georges10]

Ok merci beaucoup, bonne soirée à vous !