Bonjour chombier,
voici ma tentative de résolution.
Prenons

croissante sur

et dérivable sur
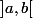
avec
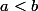
.
Supposons
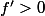
sur
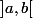
Je prétends que sous ces hypothèses, "

n'est pas strictement croissante sur

" est équivalent à "il existe un intervalle non vide et non réduit à un point

inclus dans

tel que

est constante sur

"
Sens direct : f est croissante, mais pas strictement croissante. Soit donc c<d dans [a,b] tel que
 \geq f(d))
. Par croissance de f sur l'intervalle [c,d],
 \leq f(x) \leq f(d))
Donc f est constante sur [c,d].
Sens réciproque : Soit I non vide et non réduit à un point I inclus dans [a,b] tel que f est constante sur I. Soit x<y dans I. Alors
=f(y))
, donc
 \geq f(y))
: f n'est pas strictement croissante sur [a,b]
Démontrons maintenant que "il existe un intervalle non vide et non réduit à un point

inclus dans

tel que

est constante sur

" est équivalent à "il existe un intervalle non vide et non réduit à un point

inclus dans

tel que
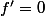
sur

"
Sens direct : Soit I non trivial tel que f est constante sur I. Soit
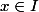
Pour h proche de 0,

et
-f(x)}{h} =0)
donc par passage à la limite
=0)
Sens réciproque : On utilise l'égalité des accroissements finis, qui provient elle même du théorème de Rolle.
(voir ce lien intéressant:
http://web.espe-guadeloupe.fr/wp-conten ... y-2009.pdf)
Soit I non trivial tel que f'=0 sur I. Soit

D'après l'égalité des accroissements finis, soit

tel que
=f(c)+(d-c)f'(e))
.
=0)
donc
=f(c))
.
Pour revenir à la question du jury, où

est un point d'accumulation de l'ensemble des zéros de

.
On peut se ramener à

et
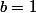
sans perte de généralité. On montre que l'ensemble des zéros ne contient aucun intervalle. Soit
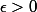
et

. Montrons qu'il existe
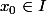
tel que
 \neq 0)
. Soit
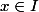
. Soit

tel que

. Alors
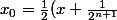)
convient.
On peut aussi dire que l'ensemble des zéros est dénombrable, donc ne contient aucun intervalle non trivial.
Donc f' ne s'annule sur aucun intervalle non trivial. Donc f n'est constante sur aucun intervalle non trivial. Donc f est strictement croissante.
