Dérivée vectorielle complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
zizzou
- Messages: 5
- Enregistré le: 24 Oct 2006, 16:01
-
 par zizzou » 30 Oct 2006, 18:43
par zizzou » 30 Oct 2006, 18:43
Bonjour,
J'aimerais calculer la dérivée de

par rapport à

sachant que

est un matrice carrée à valeurs complexe et

un vecteur colonne à valeur complexe lui aussi, le tout étant donc un scalaire.
Je trouve la réponse suivante mais elle semble fausse :
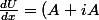x^{*} + (A - iA)^{T}x)
où le symbole

est le complexe conjugué,

est le transposé hermitien et

la transposée normale.
Si on prend le cas réel on retombe bien sur la définition dont je suis sûr :
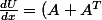x)
Merci à qui pourra m'éclairer.
-
jose_latino
- Membre Relatif
- Messages: 320
- Enregistré le: 25 Juil 2006, 21:09
-
 par jose_latino » 30 Oct 2006, 20:44
par jose_latino » 30 Oct 2006, 20:44
On a la fonction

, définie par
=x^HAx)
. Alors
v=[D(x^H)v]Ax+x^H[DA(x)v]=v^HAx+x^HAv)
. N'oublie pas que les fonctions

et

sont

linéaires. C'est ça la dérivé réelle. Il n'y a pas de dérivé complexe, la fonction

n'as pas de dérivée complexe.
-
jose_latino
- Membre Relatif
- Messages: 320
- Enregistré le: 25 Juil 2006, 21:09
-
 par jose_latino » 30 Oct 2006, 20:51
par jose_latino » 30 Oct 2006, 20:51
Si tu veux la dérivé réelle exprimée seulement en utilisant lest réelles, il faut utiliser la règle de la chaîne sur la fonction

définie par
=\xi+i\eta)
, sa dérivée est la même fonction car la fonction est linéaire (

linéaire), c'est la même chose par l'autre fonction

. La dérivée réelle est la dérivé de

, donc
(a,b)=D\psi(U(\phi(\xi,\eta)))\left(DU(\phi(\xi,\eta)\left[D\phi(\xi,\eta\right](a,b) \right)=\psi\left(DU(\phi(\xi,\eta))[\phi(a,b)] \right))
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 30 Oct 2006, 21:19
par yos » 30 Oct 2006, 21:19
Ayant développé U(x+h), je trouve
(h)=x^HAh+h^HAx)
, et je ne vois pas comment le réduire simplement. D'ailleurs le cas réel ne me semble pas donner ta formule. En résumé, il est possible que je raconte des conneries. Je regarderai de plus près si j'ai le temps.
-
jose_latino
- Membre Relatif
- Messages: 320
- Enregistré le: 25 Juil 2006, 21:09
-
 par jose_latino » 30 Oct 2006, 21:36
par jose_latino » 30 Oct 2006, 21:36
(a,b)=\psi\left(DU(\phi(\xi,\eta))[\phi(a,b)] \right)=\psi((a-ib)^TAx+x^HTA(a+ib))
,
il faut écrire
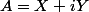
, remplacer et séparer les parties réelles et imaginaires. :++:
-
zizzou
- Messages: 5
- Enregistré le: 24 Oct 2006, 16:01
-
 par zizzou » 31 Oct 2006, 09:42
par zizzou » 31 Oct 2006, 09:42
Merci pour vos réponse.
Les solutions que vous me donnez donnent des dérivées scalaires me semble-t-il. En fait je me suis mal exprimé. Je cherche le gradiant de la fonction

. Il faut donc trouver les dérivées partielles de

par rapport à chacune des composantes de

. Le problème général étant de trouvez les extrema d'une telle fonction.
-
jose_latino
- Membre Relatif
- Messages: 320
- Enregistré le: 25 Juil 2006, 21:09
-
 par jose_latino » 31 Oct 2006, 12:07
par jose_latino » 31 Oct 2006, 12:07
Yos et moi, nous t'avons donné des les dérivés, mais elles ne sont pas de fonctionelles linéaires (donc il n'y a pas de gradient), elles sont de applications linéaires de
^2)
vers

.
jose_latino a écrit:(a,b)=\psi((a-ib)^TAx+x^HTA(a+ib)))
,
il faut écrire
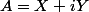
, remplacer et séparer les parties réelles et imaginaires. :++:
(a,b)=\psi((a-ib)^TAx+x^HTA(a+ib)))
(a,b)=\psi((a-ib)^T(X+iY)x+x^HT(X+iY)(a+ib)))
)
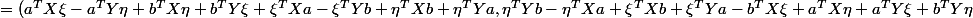)
Heureusement, il existe le MAPLE :lol2:. Si tu veux les gradients des parties réelle et imaginaire, exprimer chaque terme de la forme

ou

, la somme des tous les termes à la gauche de a ou b donnent le gradient de chaque composante. Bon courage :zen:
-
jose_latino
- Membre Relatif
- Messages: 320
- Enregistré le: 25 Juil 2006, 21:09
-
 par jose_latino » 31 Oct 2006, 12:34
par jose_latino » 31 Oct 2006, 12:34
zizzou a écrit:Merci pour vos réponse.
Les solutions que vous me donnez donnent des dérivées scalaires me semble-t-il. En fait je me suis mal exprimé. Je cherche le gradiant de la fonction

. Il faut donc trouver les dérivées partielles de

par rapport à chacune des composantes de

. Le problème général étant de trouvez les extrema d'une telle fonction.
Je me suis amusé un petit peu avec l'utilisation du MAPLE :dingue:. Mais tu cherches vraiment étudier la fonction

ou

, alors
(a,b)=U(\xi,\eta)\overline{DU(\xi,\eta)(a,b)}+\overline{U(\xi,\eta)}DU(\xi,\eta)(a,b))
\overline{DU(\xi,\eta)(a,b)}))
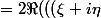^HA(\xi+i\eta) )\overline{((a-ib)^TAx+x^HA(a+ib))}))
-
zizzou
- Messages: 5
- Enregistré le: 24 Oct 2006, 16:01
-
 par zizzou » 31 Oct 2006, 12:39
par zizzou » 31 Oct 2006, 12:39
Est-ce que plus simplement il est correct d'écrire :

où le vecteur

, avec
} + \frac{\partial U}{\partial Im(x_{i})})
-
jose_latino
- Membre Relatif
- Messages: 320
- Enregistré le: 25 Juil 2006, 21:09
-
 par jose_latino » 31 Oct 2006, 12:41
par jose_latino » 31 Oct 2006, 12:41
zizzou a écrit:Merci pour vos réponse.
Les solutions que vous me donnez donnent des dérivées scalaires me semble-t-il. En fait je me suis mal exprimé. Je cherche le gradiant de la fonction

. Il faut donc trouver les dérivées partielles de

par rapport à chacune des composantes de

. Le problème général étant de trouvez les extrema d'une telle fonction.
Mais je préfère d'utiliser des méthodes de l'algèbre linéaire:

alors, il suffit de prendre les autovecteurs.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 31 Oct 2006, 19:53
par yos » 31 Oct 2006, 19:53
La différentielle DU(x) que j'ai calculé est une application linéaire de C^n dans C. Sa matrice est d'ordre nX1. C'est ça le vecteur gradient. Enfin je crois. Je me rends compte que je n'ai plus fait de différentielles depuis longtemps.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
,
, remplacer et séparer les parties réelles et imaginaires. :++:
. Il faut donc trouver les dérivées partielles de
par rapport à chacune des composantes de
. Le problème général étant de trouvez les extrema d'une telle fonction.
. Il faut donc trouver les dérivées partielles de
par rapport à chacune des composantes de
. Le problème général étant de trouvez les extrema d'une telle fonction.