Question dérivée

[HagerFall]

Bonjour,
J'ai un doute:
On a: f(x)={x*ln|x| si x/=0
{0 si x=0
La dérivée de f c'est bien:
Pour x<0:
f'(x)=1*ln|x|+x*(1/x)*(-1)=ln|x|-1
et
Pour x>0:
f'(x)=1*ln|x|+x*(1/x)*1=ln|x|+1
Juste ?

[Pseuda]

Bonjour,

Pour x<0 (comme pour x>0) la dérivée de ln|x| est 1/x.

Tu peux dire que ln|x| = ln (-x)... En dérivant, cela fait -1/(-x)=1/x.

Le 2) est bon, il y a une erreur dans le 1).

[HagerFall]

ln|x| c'est pas une fonction composée ?

[Ben314]

Salut,

ln|x| c'est pas une fonction composée ?

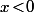
Si, mais tu as appliqué de travers la formule de dérivée d'une composée
Si et alors lorsque

[HagerFall]

Pour x<0:
On a f'(x)=ln|x|+1
et pareil pour x>0 ?

[Pseuda]

Oui, on peut le faire comme ça. La dérivée de |x| pour les x négatifs est (-1). Et la dérivée de ln x (x>0) est 1/x. Cela fait (-1)/|x|=1/x.

Pas vu le message de Ben314, je laisse.

[HagerFall]

Donc j'ai juste
f'(x)=ln|x|+1 ?

[Pseuda]

Pour x<0:
On a f'(x)=ln|x|+1
et pareil pour x>0 ?

Oui.

[HagerFall]

Ok merci

[Pseuda]

Donc j'ai juste
f'(x)=ln|x|+1 ?

Oui pour x=/= 0.

[HagerFall]

Et pour x=0 la dérivée c'est 0 ?

[Pseuda]

La fonction est-elle continue en 0 ?

En 0, pour calculer sa dérivée (éventuelle), il faut revenir à la définition avec la limite du taux d'accroissement.

[Ben314]

Avant de parler de la dérivée en x=0, ben ça serait pas con de commencer par se demander si elle existe ou pas, non ?

[HagerFall]

Bonjour,
On a: f(x)={x*ln|x| si x/=0
___________ {0 si x=0

[Pseuda]

Tu peux former le taux d'accroissement en 0 : (f(x)-f(0))/(x-0) et étudier la limite de ce rapport quand x->0 à droite, à gauche.

[zygomatique]

salut

on peut remarquer que la fonction est impaire ...