Application continue

[Kolis]

Tu écris "il existe " et tu dis qu'il n'apparaît pas ? Une révision de l'alphabet grec me semble utile !

Tu dois vouloir trouver le de ma démonstration ? Il s'agit de "alpha".
Tu peux prendre un de tes et le choisir assez petit (si tu en as un, tout réel plus petit vérifie aussi ton implication et rend supérieur à ) pour avoir .

[mehdi-128]

Donc j'ai :



Alors :

Pourquoi ne pas prendre : et ?

[mehdi-128]

Comment savez-vous que : et ?

[Kolis]

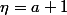
Tu ne peux pas imposer et en même temps .
De plus c'est il existe , tu ne peux RIEN supposer.

En revanche en prenant et et (çà c'est possible !) tu auras :
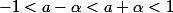
et

[mehdi-128]

Mais c'est quoi ??

J'ai en variables que : , ,

[mehdi-128]

J'ai :

Pourquoi introduire un alpha qui sort de je sais pas où ?

[Kolis]

Parce que j'en ai besoin !
Ton "eta" tu ne le connais pas (à part son existence) ! Et du coup tu ne sais pas si ton intervalle sort des bornes.
Et je te signale que TOUTES les lettres non utilisées par l'énoncé sont à ma disposition pour définir ce qui m'est utile !

Au lieu de te poser des questions existentielles tu devrais lire, comprendre puis refaire tout seul ma démonstration de 08:42 en t'appuyant sur des schémas où figurent "eta" et "alpha".

[mehdi-128]

C'est difficile !

Alors si on prend :

, , on a :



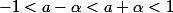
Mais comment vous obtenez :

On sait juste que :

[Kolis]

Relis, relis ...
Je "n'obtiens pas".
Je dis que SI on a ET DONC ce qui suffit pour minorer l'intégrale par

[mehdi-128]

Relis, relis ...
Je "n'obtiens pas".
Je dis que SI on a ET DONC ce qui suffit pour minorer l'intégrale par

D'accord j'ai compris l'intégrale est supérieur ou égale à mais c'est quoi la contradiction ?

On était partie de

[mehdi-128]

Ah finalement j'ai compris on a montré :

On voulait montrer : A implique B : si l'intégrale est nulle alors h est nulle

On a montré non B implique non A : si h est non nulle alors l'intégrale est > 0 donc non nulle