[MPSI] Application continue injective

[euler21]

Bonsoir.
On se donne une application I->R qui est injective et continue et le but est de démontrer que cette application est strictement monotone.
Si vous voulez réfléchir vous mêmes à l'exercice ne lisez pas la suite puisque je vais détailler mon raisonnement. Sinon je vous invite à le lire pour voir s'il est correct.
Voilà mon raisonnement:
Soit a un élément de I qui n'est pas une extrémité de I. On pose et Pour ces deux intervalles, on définit respectivement les applications g(x)=f(x)-f(a) et h(x)=f(a)-f(x). Ces deux applications ainsi définies sont continues dans leurs domaines de définitions respectifs et ne s'annulent pas puisque f est injective. Par le TVI, ces deux applications gardent nécessairement un signe constant. Supposant par exemple que g>0. un argument de continuité et de l'injectivité de la fonction f nous permet alors de montrer que f(a)0. Pour cela on raisonne par l'absurde et on suppose que h0. Donc pour tout x élément de I, si xa alors f(x)>f(a). Le choix de a étant arbitraire, on déduit alors que f est strictement croissante dans l'intervalle ouvert. On obtient qu'elle est strictement croissante dans l'intervalle I avec ses extrémités éventuelles par l'argument de la continuité et de l'injectivité.
Est ce que ce raisonnement est correct??

[Finrod]

Il m'a fallut un petit bout de temps pour comprendre la logique de ton raisonnement, mais c'est bien la même que celui du mien.

Je te le donne puisqu'il est différent.

Par l'absurde, je suppose f non strictement monotone. Cela implique soit que la dérivée s'annule sur un intervalle (absurde), soit qu'elle change de signe.

Si elle change de signe (mettons en a), on a un max ou un min. Les cas sont similaires. dans les deux cas on vérifie que l'injectivité ne peut être vérifiée.

(par ex en considérant f(a-e) et f(a+e), e petit. Par le TVI, la plus grande de ces 2 valeurs est atteinte 2 fois.

Edit En fait, ça me fait penser à un énoncé + ou - amusant, si aucun zéro de f (continue) n'est isolé et que l'ensemble des zéro de f est non vide, c'est un intervalle. On vérifie en effet que tout point situé entre 2 zéro est limite d'une suite de zéro donc par continuité est un zéro.

Pb : ça à l'air vrai sous des hypothèses plus faible que la continuité. J'imagine que pour un contre exemple, il faudrait une fonction discontinue presque partout.

SI le nombre de pts de discontinuité de f est fini, c'est ok. S'il est dénombrable, je vois à peu près comment arriver à un contre exemple.

[Ben314]

Salut,

@euler21 : ç'est o.k. moduli deux petites remarques :

a) "...Supposons par exemple que g>0. un argument de continuité et de l'injectivité de la fonction f nous permet alors de montrer que f(a)0 entraine à f(x)>f(a) par... définition de la fonction g.

b) vu que tu détaille absolument tout (à mon avis c'est même un peu trop), il ne faut pas oublier un dernier argument : en prenant ton a au début, tu as montré que
[(f(x)f(a) pour x>a)] OU BIEN [(f(x)>f(a) pour xa)].
Ce 'ou bien' résulte du fait que tu as écrit "Supposons par exemple que g>0" et que tu devrait écrire queleque part que "le cas gf(a') pour x>a')] OU BIEN [(f(x')>f(a') pour xa')].
et il faut montrer que, forcément, on est dans le même cas pour a et pour a' (ce qui est trés simple : il suffit de prendre x=a)

@Finrod : Procéder par l'absurde peut marcher (encore qu'ici, une contraposition ferait tout aussi bien l'affaire) MAIS, tu ne peut pas raisonner avec les dérivées : rien ne précise que la fonction f est dérivable.

Enfin, perso, je ferais une preuve par contraposition :
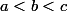
On suppose que f n'est pas strictement monotone. Cela signifie qu'il existe tels que ou bien . Dans les deux cas, il existe un y tel que le théorème des valeurs intermédiaires nous donne l'existence d'un antécédent de y dans ]a,b[ et d'un autre antécédent dans ]b,c[ ce qui montre que f n'est pas injective.

[euler21]

Salut
@ Ben314
Pour la deuxième remarque je suis tout à fait d'accord, il faut citer ce que tu as dit dans le raisonnement.
Pour la première remarque je ne vois pas comment on obtient directement le résultat puisque la fonction g n'est pas défini dans le point a.
L'argument que j'ai utilisé c'est que tque x<y on a f(x)<f(y).
En faisant tendre x vers a et puisque f est continue en a on a et puisque f est injective, l'inégalité devient stricte. Ceci étant vrai dans J, d'où le résultat.
Si la fonction présentait une discontinuité au point a, je pense pas qu'on aura le résultat.

[Ben314]

heuuuuuu, là, je ne te suis pas : rien ne dit que pour xPar contre, vu que tu as défini g(x) comme étant égal à f(x)-f(a), dire que g>0 veut dire que f(x)-f(a)>0...

[euler21]

Oui tu as parfaitement raison. Je me suis planté dans le raisonnement.
Merci pour l'éclaircissement!! :we:

[Finrod]

Oui c'est vrai, j'ai fait une contraposée et j'ai pris f dérivable. Je crois que je guérirai jamais de ce genre d'approximations, je me fais avoir à tous les coups.

Cela dit, c'était un peu inutile de passer par f' dans la mesure ou f non strictement croissante implique bien soit la constance sur un intervalle, soit un changement de pente (Dans un excès de lucidité, j'ajouterais même : qui n'annule pas nécessairement f'd et f'g (dr à droite et à gauche), comme |x|).