Classe d'un entier dans Z/bZ

[mehdi-128]

Je pense avoir trouvé : pour tout a allant de 1 à b-1, les a sont inversibles car a est premier avec b.

Ainsi les a sont inversibles on peut donc simplifier et on obtient :

Donc : donc 10^(b-1) est congru à 1 modulo b

[Pseuda]

Bonjour,

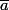
Tu as directement le produit des qui est inversible, car on est dans un groupe : (Z/bZ*, x) et tout élément est inversible.

Et c'est un groupe car justement b est premier. Par exemple, Z/6Z* n'est pas un groupe multiplicatif, car des éléments ne sont pas inversibles (trouves-en).