Ben314 a écrit:Certes, si ça ne rentre pas dans le cache écrit en alphanumérique ça va être "un peu long" (sic...)
Mais si tu compare le temps qu'il faut pour aller chercher dans la mémoire (non cache) par rapport au temps qu'il faudrait pour appliquer ta méthode, à savoir trouver le k tel que 10^k est de l'ordre du nombre en question (qui ne rentre pas dans le cache en alphanumérique...), ben je pense... que y'a vraiment, mais alors vraiment pas photo sur ce qui est le plus rapide (ou alors toi aussi tu le stocke en alphanumérique et c'est exactement la même chose : soit c'est stocké en AZT et il faut parcourir la chaine pour avoir ton k ET pour avoir le modulo 10, soit on connait d'avance la longueur de la chaine et c'est, à un poil de cul prés, la même chose de récupérer k ou le dernier chiffre)
.
Oui, c'est vrai qu'il y a la recherche du nombre de chiffre, ce qui revient à faire du modulo

Mais au pire, je peux demander à l'utilisateur d'entrer le nombre de chiffre du nombre qu'il cherche à décomposer

^^
Ben314 a écrit:Ben... faut bien lire
tout lire ce qui est écrit...
Ce que je dit, c'est que
sur le principe, ce n'est pas parce qu'un nombre est plus petit (au sens de la relation d'ordre usuelle) qu'un autre que ça prouve qu'il est plus petit au sens du nombre de

(avec

) qu'il faut pour le ramener à zéro.
Et je dit
aussi que, dans
le cas particulier où on cherche le
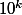
le plus "proche" (au sens du nombre d'opérations

à faire) d'un

donné, je pense (mais je suis pas 100% sûr) que là, la propriété est vraie, c'est a dire que c'est le même que le
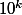
le plus "proche" au sens de la relation d'ordre usuelle.
MAIS
ça reste à démontrer (et ça me semble pas simple d'où le "pas 100% sûr") : as-tu une preuve ?
Je ne sais pas ce que je démontre c'est :
l'algorithme est optimal sur les nombre à 1 chiffre.
Supposons que l'algorithme est optimal sur les nombres k chiffres pour k < n.
Montrons alors qu'il est optimal sur les nombres à n chiffres.
Soit donc N un nombre à n chiffres.
Principe :
Soit : N= p*10^n +- r (avec p=1,2,4,8 (ou 10)) si r a un nombre de chiffre strictement plus petit que n
alors l'algorithme est optimal pour N car il ne m'a fallu qu'une seule étape pour réduire le nombre de chiffre.
et avoir une décomposition optimal pour r.
Soit N=p*10^n+- r avec r qui a le même nombre de chiffre que N alors il ne faut qu'une deuxième étape
supplémentaire pour avoir un r' sur lequel j'aurai mon hypothèse de récurrence. Et de plus dans ce cas là il
n'est pas possible de réduire le nombre de chiffre en une seule étape. (Tous ça est partie de l'idée qu'on ne peut pas faire mieux que si on avait les 10 chiffres disponibles).
.
Si j'ai montré ça alors par récurrence l'algorithme est optimal.
Donc ensuite viens toute une série d'étude cas pour le montrer :
(Je donne un exemple avec n=3, mais ça marche pour tout n) :
Les nombre de 1000 à 1500 sont les plus proche de 1000 et
a) si 1000 <= N <= 1500 alors on écrit : N = 1000 + r avec r un nombre qui a strictement moins de 4 chiffres
(une seul étape).
b) de 1501 à 1999 on a N = 2000-r avec r un nombre qui a strictement moins de 4 chiffres
(une seul étape).
c) de 2000 à 2999 on a N=2000+r avec r un nombre qui a strictement moins de 4 chiffres
(une seul étape)
d) N= 3000 on a N= 2000+1000 : optimal.
(une seule étape)
e) de 3001 à 3999 on a N=4000-r avec r un nombre qui a strictement moins de 4 chiffres
(une seule étape)
f) de 4000 à 4999 on a N= 4000+r avec r un nombre qui a strictement moins de 4 chiffres
(une seule étape)
g) de 5000 à 5500 on a : N=4000+r avec 1000<= r <= 1500 on retombe dans le cas a) qui se fait en une seule étape, donc ici il faut 2 étapes pour avoir un r' avec qui a strictement moins de 4 chiffres et on ne peut pas faire moins.
(2 étapes)
h) de 5501 à 5999 on a N= 4000 + r avec 1501 <= r <= 1999 et on tombe dans le cas b)
(2 étapes)
i) N=6000 : N= 4000 + 2000 : optimal.
(une seule étape)
etc
Bon j’arrête là parce que je dois y aller, mais en faisant tous les cas, on a une étapes quand c'est possible et que
deux sinon. (ce que je viens de faire avec n=3 marche tout aussi bien dans le cas général).
Bon après est-ce que c'est plus rapide où pas, effectivement, ce n'est pas si évident ^^.




