Montrer que E est un groupe

[Abilys38]

Bonjour à tous!

Soit * une loi de composition interne associative sur un ensemble E fini non vide.
On suppose que tous les éléments de E sont réguliers. Montrer que E est un groupe.

Un petit indice??

Je sais que je dois montrer l'existence d'un élément neutre et la symétrie des éléments, mais je ne vois pas comment...

Merci beaucoup!

[chan79]

salut
soit un élément du groupe
considère la suite
on finit par trouver deux éléments égaux

[Abilys38]

J'avais pensé à ça, mais * n'est pas forcèment une loi multiplicatrice, ça ne change rien?

[chan79]

on note multiplicativement
signifie ( étant la loi)

[Abilys38]

Alors:

Posons la suite {}
Puisque E est un ensemble fini et que * est stable dans E, nous pouvons dire que, la suite finit par contenir deux éléments égaux. Posons donc

On a alors:



Cela nous permet d'affirmer que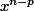 (que l'on appellera désormais ),
est l’élément neutre de E.

En effet, supposons que pour un y qui appartient à E,

On a alors: Contradiction !

Voilà le début de réponse, je cherche la suite.

[Kolis]

Bonjour !
Dire que est régulier c'est dire que est injective.
Ton ensemble étant fini l'application est aussi surjective.
Il existe alors tel que .

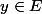De même, pour , il existe tel que 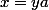. Tu en déduis que est neutre à droite.
Puis qu'il existe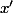 tel que . Tout élément admet un inverse à droite.

Soit tels que . Tu trouves alors que puis que ...

[chan79]

si tu supposes: n>p
soit g un élément du groupe
g*x^n =g*x^p

g*x^{n-p}*x^p =g*x^p
et par régularité à droite
g*x^{n-p}=g
on pose e=x^{n-p} ce qui fait g*e=g
et on montre qu'on a aussi: e*g=g

[Abilys38]

si tu supposes: n>p
soit g un élément du groupe
g*x^n =g*x^p

g*x^{n-p}*x^p =g*x^p
et par régularité à droite
g*x^{n-p}=g
on pose e=x^{n-p} ce qui fait g*e=g
et on montre qu'on a aussi: e*g=g

Donc en quoi mon raisonnement est faux?

[Abilys38]

Il y a deux freins qui m'empêchaient de démontrer l'inversibilité.

1) Je ne savais pas que si a est régulier, f(x) = ax est injective. Y a t-il une démonstration?
2) Je ne savais pas que si E est fini, f est bijective. Y a t-il une démonstration?

Sinon, pour la solution, c'est donc:

I/ Element neutre

Posons la suite {}
Puisque E est un ensemble fini et que * est stable dans E, nous pouvons dire que, la suite finit par contenir deux éléments égaux. Posons donc

On a alors:



Cela nous permet d'affirmer que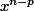 (que l'on appellera désormais ),
est l’élément neutre de E.

En effet, supposons que pour un y qui appartient à E,

On a alors: Contradiction !

II/ Inversibilité

Soit tel que f(x)= a*x
Puisque a est régulier, f(x) est injective. Par ailleurs, E est fini donc f est bijective
Nous pouvons donc poser un certain b tel que f(a*b) = e (car e appartient à E). a est inversible d'inverse b.
Nous pouvons reproduire ce raisonnement pour tous les éléments de E puisque ces éléments sont tous réguliers.

III/ Conclusion

1) * est une loi interne et associative
2) E possède un élement neutre
3) L'ensemble des élements sont inversibles

==> (E, *) est bien un groupe.



Merci!!

[chan79]

il faut aussi vérifier que quel que soit de E

[Abilys38]

il faut aussi vérifier que quel que soit de E

Mais donc le but est de montrer que est l'élement inversible non?

Pour le fait y*e=y pour tout y de E, ce que j'ai démontré par l'absurde ne suffit pas?
" En effet, supposons que pour un y qui appartient à E, ... ... Contradiction! "

Merci pour ton aide

[chan79]

tu as démontré que y=e*y
il faut démontrer aussi que y=y*e
il n'est pas dit que * est commutative

[Abilys38]

Ah oui c'est vrai! Autant pour moi.

supposons que pour un y qui appartient à E,

On a alors: Contradiction !
On a donc bien y = y*e

La même démonstration en changeant la position de e.

[chan79]

OK même si ça complique de le faire par contradiction

[Abilys38]

Oui j'ai vu ta méthode ensuite qui était plus simple mais ça aurait été du plagiat

[Abilys38]

Chan, Est ce que tu pourrais me répondre à ces deux questions? Je ne trouve rien sur internet

Il y a deux freins qui m'empêchaient de démontrer l'inversibilité.

1) Je ne savais pas que si a est régulier, f(x) = ax est injective. Y a t-il une démonstration?
2) Je ne savais pas que si E est fini, f est bijective. Y a t-il une démonstration?

3) Y a t-il une preuve à la propriété selon laquelle si f est une application inversible, elle est forcément bijective?

Merci beaucoup !!

[Ben314]

1) Je ne savais pas que si a est régulier, f(x) = ax est injective. Y a t-il une démonstration?

Ben... oui et non... vu que c'est la définition même de "a régulier".
Rappel (de définitions) :
- L'élément a du groupe G est "régulier" lorsque, pour tout x,x' de G, on a ax=ax' => x=x'.
- Une application f:X->Y est injective lorsque, pour tout x,x' de X on a f(x)=f(x') => x=x'.

2) Je ne savais pas que si E est fini, f est bijective. Y a t-il une démonstration ?

Déjà, ça, écrit texto, c'est n'importe quoi vu que pour conclure "f bijective", de "E fini", il faudrait que l'énoncé contienne un "lien" entre f et E. Ce "lien" manquant est évidement que f va de E dans E, mais ça ne suffit clairement pas à prouver la bijective de f vu que, si E a plus de 2 éléments, les applications constantes de E dans E sont non bijective.
Bref, LE résultat plus qu'archi classique, c'est que :
Si E et F sont des ensembles finis de même cardinal et si f est une application de E dans F, alors il y a équivalence entre "f injective", "f surjective" et "f bijective".
Et ça tu l'as forcément déjà utilisé de multiples fois, ne serait ce qu'en algèbre linéaire pour montrer quasiment le même résultat dans le cadre des espaces vectoriels de dim. fini et des applications linéaires.
Et il y a 36 000 façons de le démontrer plus ou moins directes (i.e. utilisant plus ou moins d'autres résultats tout aussi importants). La plus directe pourrait éventuellement être de dire que :
Si f:X->Y où X={x1,x2,...,xn} et Y={y1,y2,...,ym} sont fini, alors si on calcule le nombre d'antécédents de y1 plus le nombre d'antécédents de y2 + ... , ça fait évidement le nombre n d'éléments de X (vu que tout élément de x est l'antécédent d'un unique élément de Y).
Donc, si m=n et si f est injective, on a une somme de m=n entiers tous égaux à 0 ou 1 qui vaut n donc ils sont forcément tous égaux à 1 et f est bijective.
De même, si m=n et si f est surjective, on a une somme de n entiers tous >=1 qui vaut n donc de nouveau ils sont forcément tous égaux à 1 et f est bijective.

Et il va sans dire que, au niveau intuitif, le résultat est d'une évidence absolue : si tu colle 10 étiquettes n'importe comment sur 10 paquet (i.e. tu as une application f de l'ensemble des étiquettes dans l'ensemble des paquets) alors :
- S'il n'y a aucun paquet avec deux étiquettes ou plus alors c'est forcément que tu en a collé exactement une sur chaque paquet (i.e. injectif => bijectif)
- Si chaque paquet a au moins une étiquette, alors, de nouveau, c'est forcément que, sur chaque paquet, il y a exactement une étiquette (i.e. surjectif => bijectif)

3) Y a t-il une preuve à la propriété selon laquelle si f est une application inversible, elle est forcément bijective ?

Quelle définition donne tu à "f est une application inversible" ?
Parce que, pour moi, par définition, "f inversible", ça veut dire "f bijective", donc le moins qu'on puisse dire, c'est que la preuve, elle est comme qui dirait, pas trop compliquée...
Sinon, on peut effectivement "jouer avec les mots" en considérant que, pour une application f:E->E, "f inversible" (sous entendu pour la loi de composition interne o), ça signifie qu'il existe g telle que fog=gof=Id_E.
Dans ce cas, il me semble qu'arrivé au stade de faire de la théorie des groupes, il serait bon de quand même maitriser un tout petit peu ce qui est le B-A-BA en ce qui concerne les application entre ensembles (quelconques) et que tu as forcément déjà vu :
- D'un coté, si f est bijective, alors elle admet une "bijection réciproque" f^-1 qui, justement, vérifie fof^-1 = f^-1 o f =Id_E.
- Dans l'autre sens, si fog=Id_E alors fog est surjective, donc f est surjective et, d'un autre coté, le fait que gof=Id_E implique que gof est injective donc que f est injective.

P.S. : Désolé si je te vexe, mais je suis quand même réellement abasourdi que quelqu'un qui fasse de la théorie des groupes puisse poser ce genre de question totalement élémentaires et qui, normalement, sont sensés être parfaitement acquis à l'issue du L1.

[Abilys38]

Ok merci beaucoup! J'ai très bien compris la démonstration.
Donc, dans l'exercice ce qui permet d'affirmer que f est bijective, c'est que, au préalable, on a démontré que f était injective !
Effectivement ma manière de poser la question était loin d'être bonne.

Donc la propriété est la suivante?

Soit f une application de E -----> E tel que f est injective (resp. surjective) et E un ensemble fini. f est surjective (resp. injective) et bijective.

Ou encore f une application de E dans F tel que E et F ont un même nombre fini d’éléments.

[Abilys38]

Pour la propriété 3), merci pour tes explications qui sont parfaitement claires encore une fois.
En fait je suis en premier semestre de MPSI, et je dois avouer que j'ai fais le chapitre sur les applications en tout début d'année, avec des méthodes de travail qui n'étaient encore pas très bonnes.

Je savais que une fonction bijective admettait pas définition une réciproque, mais j'avais complétement oublié le théorème selon lequel toute application qui admet une application réciproque est bijective.

[Ben314]

Le chapitre concernant les applications "ensemblistes" (injection, surjections, ensembles finis), il est totalement indispensable à tout les autres chapitres d'algèbres.
C'est légèrement moins vrai pour les chapitres d'analyse où la notion de bijection est un peu moins omniprésente, mais même en analyse, c'est une notion qui revient très très souvent.
Enfin, bref, parmi les "briques élémentaires" des maths, c'est indiscutablement celle qu'on utilise le plus souvent.