Cardinal quantitatif et autres travaux mathématiques (1)

[Robot]

Pour enseigner au CNED, il faut au moins le CAPES.

[Robot]

Pour les recrutements au CNED :

http://www.cned.fr/media/701818/enseignant-cned-2014.pdf

[Robot]

N'as-tu pas remarqué que c'est dans la section "VOUS ETES ENSEIGNANT TITULAIRE DE L’EDUCATION NATIONALE" ?

[Pseuda]

N'as-tu pas remarqué que c'est dans la section "VOUS ETES ENSEIGNANT TITULAIRE DE L’EDUCATION NATIONALE" ?

C'est une aberration :

L'oral du CAPES ne sert, strictement, à rien, dans la sélection, dans le recrutement, pour les postes adaptés au CNED :

Je dirais même qu'une proportion non négligeable de ceux qui prétendent aux postes adaptés, se feront d'avantage éliminer à l'oral, alors que celui-ci ne sert à rien dans le cadre d'un poste au CNED, qui est avant tout un poste et un métier d'écrit.

Ne crois pas que l'oral du CAPES sert uniquement à éprouver les capacités orales du candidat. Les leçons d'oral consistent (ou du moins consistaient quand j'ai passé le CAPES en 99) à approfondir le programme du secondaire - 1ère année post-bac pour voir toutes les notions sous tous leurs aspects. Tout le programme du secondaire est démontré, décortiqué, une même notion est vue sous différentes approches (par exemple, la fonction exponentielle est introduite de plusieurs manières différentes et on démontre l'équivalence de ces approches). Des chapitres qui ne sont pas au programme du secondaire aujourd'hui mais qui l'ont été ou qui le seront peut-être dans le futur, sont étudiés. Bref rien n'est laissé au hasard.

Cela me permet très normal qu'un professeur au CNED qui ne travaillera dans le secondaire qu'à l'écrit soit titulaire du CAPES.

[Pseuda]

L'enseignement au collège est tellement élémentaire, basique, rudimentaire et rasoir, que quasiment tout étudiant en mathématiques qui se respecte, possède, nécessairement, les connaissances nécessaires :

Par contre, tout étudiant en mathématiques, même voire un titulaire du CAPES, ne possède pas nécessairement les bases de la pédagogie ni celles de la gestion de classe.

Il faut posséder et maîtriser, un peu plus de connaissances pour enseigner au lycée, mais fondamentalement, pour un étudiant en mathématiques, ce n'est pas très sorcier, et ces connaissances ou bien on les a, ou bien on se les réapproprie très vite.

Le métier (en classe) s'apprend, essentiellement et avant tout, sur le tas et avec l'expérience (surtout avec le peu de formation qu'on reçoit).

Détrompe-toi. Quand on commence à enseigner, on n'a pas le temps de se réapproprier des connaissances, on ne fait plus que de la gestion de classe, de la préparation des cours, mise au point des contrôles, correction des DM et DS, réflexion sur la pédagogie, gestion de l'humain dans la classe (motivation des élèves, gestion des conflits...), relation avec les collègues et le principal ou le proviseur, conseils de classe, réunion parents-professeurs... tout cela prend énormément de temps.

On pourrait tout aussi bien être prof d'histoire-géo.

Honnêtement, lors de l'épreuve orale de leçon du CAPES externe, tu n'as pas le temps de faire un vrai cours et les exigences des oraux, sont à des années lumières de celles réellement exigées et nécessaires pour exercer le métier (en classe).

Si, tu peux faire un vrai cours lors de l'épreuve orale du CAPES, en accéléré. Hum je rectifie ce que j'ai écrit plus haut :
L'oral du CAPES porte (ait) essentiellement sur le programme de TeS (et à travers lui, sur tout le secondaire), et sur la 1ère année post-bac, et sur du hors-programme de tout (que j'ai découvert).
Ce ne sont pas des années-lumière. Quand tu commences à enseigner, tu te rends compte qu'il faut être très rigoureux, bien plus qu'en travaillant pour soi. (c'est bien plus compliqué que de savoir juste faire les exercices).

Par contre, tout étudiant en mathématiques, même voire un titulaire du CAPES, ne possède pas nécessairement les bases de la pédagogie ni celles de la gestion de classe.

Je suis tout à fait d'accord, on n'est pas préparé à cela lors des études de maths.

Tu peux aussi te tourner vers les cours particuliers (pas de gestion de classe, tu peux préférer la relation seul à seul). Il y a une très forte demande (je peux en témoigner), mais par contre c'est très mal rémunéré.

[bolza]

A Ben314 et bolza,

Dans mes travaux, il y a pour le moment, une forteresse en béton armé à abattre

et des efforts d'intuition et de préformalisation,

de nature encore inconnue voire inédite voire de l'ordre de l'indicible et de l'inexprimable,

à fournir, intensément et massivement ,

avant de pouvoir aboutir à quelque chose de véritablement potable et exprimable de façon intelligible,

c-à-d à une formalisation finale parfaite et aboutie.

Mais Ben314 et bolza, ne veulent absolument pas entendre parler des ces stades et de ces étapes intermédiaires, très informelles :

Ils ne veulent que la formalisation finale.

Comment ????

Je trouve que tu as un sacré toupet de dire ça :
Combien de fois on t'a demandé de t'exprimer avec des mots SANS utiliser le formalisme mathématiques ne serait ce que pour avoir au moins une chance de savoir quel est ton intuition ?????

Et combien de fois tu t'est obstiner TOI à n'utiliser que le formalisme mathématiques
soit-disant que tes "symboles parlent d'eux même". Si on te dit qu'on ne comprend pas ce que signifie ces symboles c'est que de toute évidence, pour nous ils ne parlent pas suffisamment d'eux même.

La dernière fois je t'ai demandé de m'expliquer avec des mots sur des objets simple : segment, droite, ...
mais la seule chose que tu a trouvé à faire, c'est de te défiler encore une fois en me ressortant tes pdf.

Quand comprendra tu que quand on est dans le formalisme mathématiques, on est dans la rigueur, la précision. Mais quand on est au stade de l'intuition ou des idées, alors on est encore dans les mots, les exemple, les concepts ?

Mais bref, passons, voici une dernière tentative (vaine, malheureusement)
pour essayer de te convaincre que ta notion de cardinal est problématique :

Pour résumer la seule chose que j'ai compris de tout le charabia que tu nous a sorti depuis ces 14 pages
de discussion c'est que tu veux un "cardinal" tel que si A est strictement inclus dans B alors le "cardinal" de A
est strictement plus petit que le "cardinal" de B.


Je trace une droite pour représenter les réels.
Question : Où places-tu le 0 sur la droite ?

[bolza]

Je trace une droite pour représenter les réels.
Question : Où places-tu le 0 sur la droite ?

Tu choisis par convention, un point arbitraire de la droite, et tu t'y tiens.

Donc je prend mon crayon bleu, je marque un point que je choisi et que je vais noté 0.
Je prend mon crayon rouge, et je place un point à droite du point bleu.
Soit A l'ensemble des points de la droite qui sont à gauche du point bleu.
Soit B l'ensemble des points de la droite qui sont à gauche du point rouge.

On a :
a) "cardinal(A)"= "cardinal()" car par convention le point bleu est 0.
b) "cardinal(A) < cardinal(B)" car A est strictement inclus dans B.
et donc en particulier "cardinal(B)" est différent de "cardinal()".

Maintenant comme annoncer précédemment, le fait que le point bleu représente le 0 est un choix
complètement arbitraire. Autrement dit, j'aurais très bien pu décidé que le point rouge représente 0.
et dans ce cas on a :

c) "cardinal(B)"= "cardinal()" (par convention).

Ce qui contredit totalement le b).

Tu remarquera que les ensembles A et B sont défini indépendamment de la convention choisis.
Et que dans les deux cas on trouve des résultats différents pour "cardinal(B)".

Il y a donc un souci.

[bolza]

Je crois que ma théorie règle ce genre de problème :


Puisque, dans celle-ci , on a :



et

et

1) il dit qu'il voit pas le rapport.

2) ???!?!???
juste trois question pour être sûr :
c'est bien l'ensemble des entiers naturels tel que tout le monde connais ?
c'est bien le même "+" que dans ?
c'est bien le nombre 1, le successeur de 0, le ?
et j'ai aussi envie de te demander, aller juste pour voir avec des mots, ça veut dire quoi ?
Comprend tu ce que l'on veut dire par "ce que tu écris n'a pas de sens" ?

EDIT : En réfléchissant un peu le seul sens que je peux trouver à c'est : "l'ensemble des entiers naturels auxquels on a ajouté 1".

Si c'est cela alors :

1) c'est bien de le préciser avec des mots, au moins on comprend tout de suite ce que ça veut dire, car ce que tu as utilisé ici, c'est ce qu'on appelle un abus de notation, et c'est toujours mieux de préciser quand on en utilise.
2) J'ai le regret de t'annoncer que

[bolza]

et j'ai aussi envie de te demander, aller juste pour voir avec des mots, ça veut dire quoi ?

Dans ma théorie, on a :

J'ai rien compris (qu'est ce que tu ne comprend pas dans "avec des mots" ??)
Mais ça n'a aucune importance :

1) il dit qu'il voit pas le rapport.

[bolza]

1) il dit qu'il voit pas le rapport.

[bolza]

Rappel :

Je trace une droite pour représenter les réels.
Question : Où places-tu le 0 sur la droite ?

Tu choisis par convention, un point arbitraire de la droite, et tu t'y tiens.

Donc je prend mon crayon bleu, je marque un point que je choisi et que je vais noté 0.
Je prend mon crayon rouge, et je place un point à droite du point bleu.
Soit A l'ensemble des points de la droite qui sont à gauche du point bleu.
Soit B l'ensemble des points de la droite qui sont à gauche du point rouge.

On a :
a) "cardinal(A)"= "cardinal()" car par convention le point bleu est 0.
b) "cardinal(A) < cardinal(B)" car A est strictement inclus dans B.
et donc en particulier "cardinal(B)" est différent de "cardinal()".

Maintenant comme annoncer précédemment, le fait que le point bleu représente le 0 est un choix
complètement arbitraire. Autrement dit, j'aurais très bien pu décidé que le point rouge représente 0.
et dans ce cas on a :

c) "cardinal(B)"= "cardinal()" (par convention).

Ce qui contredit totalement le b).

Tu remarquera que les ensembles A et B sont défini indépendamment de la convention choisis.
Et que dans les deux cas on trouve des résultats différents pour "cardinal(B)".

Il y a donc un souci.

Pour résumé je défini deux demi-droite A et B à partir d'une droite sensé représenter la droite des réels.
Ensuite pour placer le 0 je fais 2 choix de convention :

convention 1) : "cardinal(B) différent de cardinal(R-)"
convention 2) : "cardinal(B) égal cardinal(R-)"

Il y a un problème, n'est-ce pas ?

[bolza]

1) il dit qu'il voit pas le rapport.

Le raisonnement que tu as fait, est tout simplement faux.

L'origine qu'on se fixe au départ, a une importance cruciale.

Une fois l'origine choisie fixée, on ne peut pas en choisir une autre arbitrairement (comme si de rien n'était)

Donc, je me suis trompé, aussi.

Non, car les ensembles A et B sont définis indépendamment de la convention choisi.

[bolza]

Si cette histoire de changement de convention te gêne voici la situation suivante :

Je donne à Alfred et Bob le dessin de la même droite avec les points rouge et bleu au même endroit.
et avec les définitions des ensembles A et B. Je leur demande ce qu'ils pensent du "cardinal(B)".

Alfred et Bob travaillent indépendamment.

Alfred choisi comme convention "Le point bleu représente 0".
Bob qui n'est pas au courant de ce que fait Alfred, lui a choisi comme convention "Le point rouge représente 0".

Alfred trouve que : "cardinal(B) > cardinal(R-)"
Bob trouve que : "cardinal(B) = cardinal(R-)"

Qui a raison ?

En tous cas il ne peuvent avoir raison tous les deux.
Et si un des deux à raison ça veut dire qu'une des deux convention n'est pas correcte,
mais alors on en reviens à ma question de départ :
Si des conventions sont correctes et d'autre non, comment puis-je déterminer quelle est la bonne convention ?
Autrement-dit : Mon point 0 je le place où ?

Personnellement je trouve beaucoup plus absurde que l'emplacement du points 0 sur la droite des réels
ait une importance que deux ensembles infini dont l'un est strictement inclus dans l'autre aient "autant"
d'éléments, car quand on réfléchi un peu sérieusement sur ce qu'est l'infini, on s'aperçoit que ce n'est pas si choquant que ça.

P.S : Tu peux retrouver le même problème différemment :

Si deux ensembles superposables ont même "cardinal" alors ça implique que toutes
les demi droites ont même "cardinal"(*). Ce qui est en contradiction avec le fait que A strictement inclus B -> "cardinal(A) < cardinal(B)".

(*) car toutes les demi-droites sont superposables.

[Robot]

Dans l'un des pdf auxquels notre ami se réfère (et qui n'est pas de lui), on trouve cette axiomatique pour une application 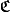d'une classe de parties de à valeurs dans un anneau commutatif ordonné (je recopie) :
1)
2)
3)
4) Si est l'image de par un déplacement, .
5)
6)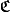 est continu (à préciser)
7)
Il apparaît que c'est une approche mathématique bien établie, et qui a un contenu non trivial pour certaines classes intéressantes de parties de . Il semble que notre ami tourne en rond en essayant d'étendre ceci à des situations où ça ne fait plus sens. Il utilise un empilement de notations absconses qui ne réussit pas à camoufler l'incohérence de ce qu'il écrit.

[bolza]

Et Comment déterminer qui a raison entre Alfred ou Bob ?

Et tu as oublier cette partie là :

P.S : Tu peux retrouver le même problème différemment :

Si deux ensembles superposables ont même "cardinal" alors ça implique que toutes
les demi droites ont même "cardinal"(*). Ce qui est en contradiction avec le fait que A strictement inclus B -> "cardinal(A) < cardinal(B)".

(*) car toutes les demi-droites sont superposables.

Dans ma théorie, toutes les distances infinies, ne se valent pas.

Donc, ma théorie dépend du repère choisi :

C'est la seule concession à faire.

Tu pense sérieusement qu'une théorie où un simple changement de répère modifie le "cardinal"
de tes ensembles puissent être une théorie cohérente où même viable ?

[Robot]

Non, je suis convaincu qu'il existe bien une manière de le faire.

Une conviction qui ne repose sur aucun fondement, et ce que tu écris ne montre absolument aucune avancée dans cette direction.

[bolza]

Dans ma théorie, 2 "demi-droites", ne sont pas forcément superposables :

Une "demi-droite" particulière peut être strictement plus courte qu'une autre :

Non, le fait que deux demi-droites soient superposables, n'a rien à voir avec ta théorie, c'est un théorème
de géométrie. Il suffit d'une translation et d'une rotation pour superposer deux demi-droite.
(Donc déjà pour un "cardinal" invariant par translation ou rotation c'est raté). Et ne me parle pas
de l'axiome du choix ici, il n'a rien à voir la dedans.

Tu pense sérieusement qu'une théorie où un simple changement de répère modifie le "cardinal"
de tes ensembles puissent être une théorie cohérente où même viable ?

Oui, tout à fait :

Un changement de repère ne peut modifier que le cardinal quantitatif des ensembles non bornés, pas celui des ensembles bornés.

Donc à la question : lequel de Alfred ou Bob a raison, ta réponse est les deux ?
ça veut dire que à un même ensemble infini B, on peut donner pour "cardinal(B)"
la "valeur" de "deux nombres infini" différents ?

Si tu ne vois pas de l'incohérence là dedans alors tant pis pour toi.
Bon courage pour la suite.

[Pseuda]

Bonjour,

C'est vrai qu'un certain savant, après une scolarité médiocre, un retard scolaire (dyslexie...), des résultats décevants à l'école polytechnique de Zurich (où il n'a été accepté qu'au deuxième essai), s'est retrouvé, après une période de chômage, à l'Office fédéral des brevets de Berne, ... , avant de devenir un des plus grands génies de tous les temps :

http://www.linternaute.com/biographie/albert-einstein/
https://savoir.actualitte.com/article/s ... venu-genie

Comme quoi, tout est possible, tout est permis, il ne faut pas désespérer, il ne faut pas baisser les bras, au contraire...

[Pseuda]

Bonjour,

Je n'ai toujours pas entre-ouvert tes documents, vue la réaction des uns et des autres à leur lecture, arrêtés dès les premières lignes par des définitions qu'ils ne comprennent pas, (et par un style, dirons-nous, un peu égocentrique),

Mais t'es-tu seulement demandé si ton problème avait, au moins intuitivement, une solution.

Car enfin, tel que je l'ai compris (mais je peux avoir très mal compris), tu cherches un cardinal (quantitatif) à mettre à chacun des ensembles qui comportent le même "nombre" d'éléments, mais es-tu sûr que R à lui tout seul est suffisant ?

En effet, il faut un cardinal pour N, un autre pour N-{1}, un autre pour N-{1,2}, un autre pour N-{1,2,....n } pour tout n, idem pour Z, Z-{1} (ce n'est pas le même que celui de N-{1}), ..., Q, ..., R, R-{1}, R-toute partie de R à laquelle on rajouterait "un par un" chaque élément de R, soit "autant" que R comporte de nombres. Donc cet ensemble qui comporterait les cardinaux quantitatifs des ensembles inclus dans R, serait "un miroir" de R, donc aucun intérêt.

Il faut d'autres cardinaux pour , , etc..., soit "autant" que , comportent de nombres. Tu vois ce que je veux dire ?

Désolée de te faire redescendre sur terre, mais, plus j'y réfléchis, plus j'ai la conviction que ton problème, tel qu'il est parti (enfin tel que je le perçois) n'a pas de solution : pour loger ces "cardinaux quantitatifs", il faudrait un ensemble plus grand que tous les ensembles existants, ça se mord la queue, donc c'est impossible (au vu de mes connaissances).

Mais peut-être que ton but n'est pas de trouver une solution à ce problème....

Pour Einstein, ne pas savoir parler à 3 ans, ni même à 4, cela ne veut rien dire, j'ai un exemple près de moi. Tu as peut-être raison, il a pris cet emploi pour pouvoir être plus tranquille.

[Pseuda]

Je ne comprends rien. Bon courage !