Congruence
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
toto273
- Membre Naturel
- Messages: 32
- Enregistré le: 23 Sep 2015, 15:18
-
 par toto273 » 28 Oct 2015, 17:55
par toto273 » 28 Oct 2015, 17:55
Bonjour, pourriez-vous m'aider à prouver que si
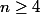
,
)
, s'il vous plaît ?
Merci d'avance

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 28 Oct 2015, 18:06
par capitaine nuggets » 28 Oct 2015, 18:06
Salut !
C'est bizarre : pour
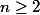
, ça marche...
Il suffit de savoir que
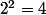
et que

signifie que

est multiple de

...
:+++:
-
toto273
- Membre Naturel
- Messages: 32
- Enregistré le: 23 Sep 2015, 15:18
-
 par toto273 » 28 Oct 2015, 18:36
par toto273 » 28 Oct 2015, 18:36
D'accord, merci beaucoup, j'ai compris ! Est-ce que vous pourriez également m'aider à prouver que
^{2}\equiv2(4))
, avec
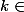

. Merci !
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 28 Oct 2015, 18:38
par nodjim » 28 Oct 2015, 18:38
9=1 mod 4
(2k+1)²=4k²+4k+1=1 mod 4.
1+1=2
-
toto273
- Membre Naturel
- Messages: 32
- Enregistré le: 23 Sep 2015, 15:18
-
 par toto273 » 28 Oct 2015, 18:40
par toto273 » 28 Oct 2015, 18:40
D'accord, merci, mais pourquoi 4k²+4k+1=1 mod 4 ?
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 28 Oct 2015, 18:44
par nodjim » 28 Oct 2015, 18:44
Parce que 4k²=0 mod 4 (le reste de la division par 4 de 4k² est 0) et pareil pour 4k.
-
toto273
- Membre Naturel
- Messages: 32
- Enregistré le: 23 Sep 2015, 15:18
-
 par toto273 » 28 Oct 2015, 18:48
par toto273 » 28 Oct 2015, 18:48
D'accord, merci beaucoup !
-
toto273
- Membre Naturel
- Messages: 32
- Enregistré le: 23 Sep 2015, 15:18
-
 par toto273 » 28 Oct 2015, 20:36
par toto273 » 28 Oct 2015, 20:36
Et en quoi le fait que
^{2}\equiv2(4))
et
)
, implique que
^{2}=2^{n})
n'a pas de solution, s'il vous plaît ?
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 29 Oct 2015, 08:28
par nodjim » 29 Oct 2015, 08:28
9+(2k+1)² = 2 mod 4, c'est à dire que c'est divisible par 2 une seule fois, et donc ne peut être une puissance de 2 supérieure à 2, et en particulier ne peut être divisible par 4. Alors que 2^n, pour n>1, est évidemment divisible par 4. Une fois qu'on a vérifié que le plus petit 9+(2k+1)² n'est pas égal à 2, on a fini.
OK ?
-
toto273
- Membre Naturel
- Messages: 32
- Enregistré le: 23 Sep 2015, 15:18
-
 par toto273 » 29 Oct 2015, 11:45
par toto273 » 29 Oct 2015, 11:45
D'accord, merci beaucoup, j'ai peut-être compris !
Donc en gros pour résumer, comme
^{2})
et
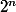
ne congruent pas vers le même nombre modulo 4, ça signifie que l'équation n'a pas de solution ?
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 29 Oct 2015, 11:51
par nodjim » 29 Oct 2015, 11:51
Exactement. Si 2 nombres n'ont pas les mêmes restes par division par un même diviseur, alors ils ne sont pas égaux. L'inverse n'est pas pour autant vrai: si 2 nombres ont le même reste quand ils sont divisés par le même diviseur, ils ne sont pas pour autant forcément égaux.
-
toto273
- Membre Naturel
- Messages: 32
- Enregistré le: 23 Sep 2015, 15:18
-
 par toto273 » 29 Oct 2015, 11:55
par toto273 » 29 Oct 2015, 11:55
D'accord, merci beaucoup !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 91 invités
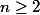 , ça marche...
, ça marche...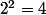 et que
et que  signifie que
signifie que  est multiple de
est multiple de  ...
...
