Équation second degré congruence

[Theop54]

Bonjour,
Je suis sur un Dm de spé math depuis quelque temps mais j'ai un tout petit problème de logique, voici le sujet :

En étudiant les carrés modulo 8, résoudre dans Z l'équation x²+4x-4;)0(8)

J'ai multiplié les deux membres par 2, ce qui revient à résoudre 2x²;)0(8)
A partir de là, il y a deux choix pour moi ; soit x²;)0(8) car si x²;)0(8) alors 2x²;)0(8), soit x²;)4(8)
car si x²;)4(8) alors 2x²;)8;)0(8)

J'ai fais un tableau de valeur de x²;)...(8) pour x allant de 0 à 7 ( pour répondre à la première partie de la question ), puis j'ai généralisé et j'ai montré que pour k€Z, si x=8k et x=8k+4 alors x²;)0(8) et donc ce sont deux solutions, et aussi que si x=8k+2 ou x=8k+6 alors x²;)4(8) et donc solutions.

Le problème est que si x²;)0(8) les résultats marchent pour 2x²+8x-8;)0(8) mais pas pour x²+4x-4;)0(8) car je ne trouve pas un nombre entier et peux le démontrer...ce que je ne comprends pas c'est pourquoi les deux ne marchent pas ensemble puisque j'ai suivis les règles de calculs...résoudre x²+4x-4;)0(8) devrais être aussi résoudre 2x²+8x-8;)0(8)

Voilà, petit problème mais qui m’embête :crash:

[Ben314]

Salut,
Déjà, dés le départ, ça déconne : dire que (A congru à B modulo 8), ça veut dire que A=B+8k avec k dans Z et, si tu multiplie par 2, ça donne 2A=2B+16k, c'est à dire .
Donc ça sert pas a grand chose vu que, modulo 16, tes 8 ne s'éliminent pas.

A mon avis, ce qui est attendu, c'est plutôt une mise sous forme canonique du trinôme...

Si tu veut voir les chose un peu différemment, il est vrai que :
Si alors pour tout entier 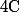on a
Mais la réciproque est fausse, par exemple est congru à modulo 8, mais 9 n'est pas congru à 5 modulo 8.

[nodjim]

modulo 8, x² + 4x - 4 = x² + 4x + 4 = (x+2)²
Du coup, ça marche pour 2 et 6.

[chan79]

Fais un tableau qui te donne les valeurs de x²+4x-4, modulo 8, quand x varie de 0 à 7

[Theop54]

Salut,
Déjà, dés le départ, ça déconne : dire que (A congru à B modulo 8), ça veut dire que A=B+8k avec k dans Z et, si tu multiplie par 2, ça donne 2A=2B+16k, c'est à dire .
Donc ça sert pas a grand chose vu que, modulo 16, tes 8 ne s'éliminent pas.

A mon avis, ce qui est attendu, c'est plutôt une mise sous forme canonique du trinôme...

Si tu veut voir les chose un peu différemment, il est vrai que :
Si alors pour tout entier on a
Mais la réciproque est fausse, par exemple est congru à modulo 8, mais 9 n'est pas congru à 5 modulo 8.

Je me disais qu'avec les congruences il y aurait un truc que j'allai oublié...merci de me rafraichir la mémoire ^^
La forme canonique est donc (x+2)²-8, ce qui revient à résoudre (x+2)²;)0(8)

modulo 8, x² + 4x - 4 = x² + 4x + 4 = (x+2)²
Du coup, ça marche pour 2 et 6.

J'avais penser aux identités remarquables mais je ne voyais pas comment l'obtenir...du coup on en revient à une simple équation, soit x+2;)0(8) donc x;)-2;)6(8) ce qui fait 8k+6, soit x+2;)4(8) cad x;)2(8) et donc x=8k+2..0

Donc si je ne me trompe pas, on n'a pas utilisé les carrés modulo 8, ce n'est peut-être pas la méthode attendue ? En tout cas merci, ça résout quand même le problème !

[Ben314]

Non, c'est encore raté....
Parmi les pièges des congruence, celui dont il faut le plus se méfier, c'est que le résultat vrai dans R qui dit que "un produit est nul si et seulement si un des facteurs est nul" eh bien il est faux avec les congruence : ni 2 ni 3 ne sont nuls modulo 6 et pourtant le produit 2x3 est nul modulo 6.
Et même lorsque les deux nombre du produit sont les mêmes, c'est à dire qu'on a x²=0, ben ça implique pas que x=0.
Par exemple 4 est non nul modulo 16 alors que 4² est nul modulo 16.

BILAN : de (x-2)²=0 mod 8, tu ne peut pas déduire que x-2=0 modulo 8.
Dresse la tables des carrés modulo 8 et tu verra qu'il y a un nombre autre que 0 dont le carré est nul.

Je pense que tu devrais voir d'ici quelques temps que, pour que quasiment tout fonctionne comme dans R (en particulier qu'un produit soit nul ssi un des facteur est nul), il faut faire des congruences modulo un nombre premier (sauf que 8, c'est pas un nombre premier...)

[Theop54]

J'ai déjà fais ce tableau et pour x=4, x²;)0(8)
Il faut donc dire qu'on veut trouver x pour que x+2 soit égal à 8k ou 8k+4 car si x=8k ou 8k+4 alors x²;)0(8) et donc x+2 serait congru à 0 modulo 8 et l'équation serait vérifiée ?
Je pense avoir compris, mais je ne pense pas l'expliquer convenablement.

On a commencé les bases des PGCD donc on va les faire dans pas longtemps les nombres premiers je pense ^^

[Ben314]

Vu le "En étudiant les carrés modulo 8..." de l'énoncé, je pense que ce qui est attendu, c'est d'abord de dire que x²+4x-4;)0(8) équivaut à (x+2)²;)0(8) puis, en dressant la table des carrés modulo 8, de voir que t²;)0(8) si et seulement si t;)0(8) ou t;)4(8)

[nodjim]

(x+2)²=0 [8]
Tu peux analyser la parité:
Il faut au moins que x+2 soit pair, donc x pair.
Mais il faut en plus que ce soit "3 fois pair". Si x+2 est seulement divisible par 2 alors son carré n'est divisible que par 4, ce qui ne convient pas. Il faut donc que x+2 soit divisible par 4.

[Theop54]

Vu le "En étudiant les carrés modulo 8..." de l'énoncé, je pense que ce qui est attendu, c'est d'abord de dire que x²+4x-4;)0(8) équivaut à (x+2)²;)0(8) puis, en dressant la table des carrés modulo 8, de voir que t²;)0(8) si et seulement si t;)0(8) ou t;)4(8)

Je vois, dernière question, doit-on faire tous les cas en écrivant t=8k, t=8k+1,...,t=8k+7 pour démontrer que selon les valeurs de t, si t=8k et t=8k+4 alors t²;)0(8) ? Si oui ça ne prends que 8lignes mais ça peut être long en DS.

(x+2)²=0 [8]
Tu peux analyser la parité:
Il faut au moins que x+2 soit pair, donc x pair.
Mais il faut en plus que ce soit "3 fois pair". Si x+2 est seulement divisible par 2 alors son carré n'est divisible que par 4, ce qui ne convient pas. Il faut donc que x+2 soit divisible par 4.

Si x+2 doit être divisible par 4 alors x+2;)0(4) ==> x+2=4k ==> x=4k-2 mais cela rassemble-t-il toutes les valeurs possibles ?

[Ben314]

Perso, je ferais juste un tableau avec deux lignes :
Ligne 1 : T modulo 8 = 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7
Ligne 2 : T² modulo 8 = ....

[nodjim]

C'est bien sûr une méthode passe partout qui marche toujours. Mais si la question était
x² + 64x - 1024 = 2048, ce serait un peu long.

[Ben314]

Tout à fait, et c'est d'autant plus couillon dans le contexte présent qu'avec un tableur, on aurais pas mis beaucoup plus de temps à faire directement un tableau avec :
Ligne 1 : X modulo 8 = 0 , 1 , 2 , ... , 7
Ligne 2 : X²-4X-4 modulo8 = ...

Mais comme l'énoncé dit "En étudiant les carrés modulo 8 ...", il faut bien en faire quelque chose.

Et concernant le fait de faire ou pas un tableau pour les carrés, c'est effectivement la "petitesse" du 8 de l'énoncé qui me fait supposer que c'est juste un tableau qui est attendu, ce qui n'empêche évidement pas d'essayer de trouver une meilleure méthode qui fonctionnerais avec des valeur plus grandes.

[Theop54]

Effectivement pour les valeurs plus grandes on risque d'y passer un petit moment...il y a peut-être une histoire de PGCD ou de nombre premier comme tu me l'a dit mais je vais déjà penser à finir mon DM avant le nouvel an : p

En tout cas merci de votre aide...on peut facilement se perdre avec ces congruences au début !