Suites

[Elsapseudo]

Bonjour à toutes et à tous,

Soit (un) la suite définie par u0= -2 et la relation un+1=(1/2)un +3.

Je dois démontrer que un<6 pour tout entier naturel n.

Comment faire?

Merci d'avance!

[capitaine nuggets]

Salut !

Tu peux toujours raisonner par récurrence :++:

[mathelot]

bonjour,

utilise la croissance sur de
pour obtenir l'hérédité de

[Elsapseudo]

Salut !

Tu peux toujours raisonner par récurrence :++:

Quel autre moyen a part résonner par récurrence?

[capitaine nuggets]

A priori, à part exprimer en fonction de , je ne vois pas d'autres moyens.

Pour exprimer , on va avoir besoin d'une suite auxiliaire :
Considère la suite définie par .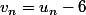
Montre que est géométrique.
Déduis-en en fonction de , puis en fonction de .
Essaye alors de montrer ton inégalité.

:+++: