Nouvelle formule pour convertir les bases?
21 messages
- Page 1 sur 2 - 1, 2
Nouvelle formule pour convertir les bases?
Bonjour tout le monde!
Comme le précise le titre, je penses avoir découvert une nouvelle formule pour convertir les nombres de base 10 vers une base inférieure. J'ai cherché sur internet, sur des forum, des cours, etc. si ma formule existait, mais je n'ai rien trouvé.
D'où, pour en être sûr, je vous demande de partager vos connaissance en conversion de base.
De plus, j'ai fais des test sur ma formule: comparer la vitesse de ma formule avec la méthode basique de conversion, et j'ai trouvé que ma formule était plus rapide.
Bien que je sois content, je me demande aussi si l'utilité d'une nouvelle formule est grande. Donc je vous demande à tous de dire ce que vous pensez ma formule.
Ne soyez pas surpris si je ne poste pas la formule elle-même: je ne sais pas encore quoi faire de ma formule encore.
Merci d'avance!
Silver.
Comme le précise le titre, je penses avoir découvert une nouvelle formule pour convertir les nombres de base 10 vers une base inférieure. J'ai cherché sur internet, sur des forum, des cours, etc. si ma formule existait, mais je n'ai rien trouvé.
D'où, pour en être sûr, je vous demande de partager vos connaissance en conversion de base.
De plus, j'ai fais des test sur ma formule: comparer la vitesse de ma formule avec la méthode basique de conversion, et j'ai trouvé que ma formule était plus rapide.
Bien que je sois content, je me demande aussi si l'utilité d'une nouvelle formule est grande. Donc je vous demande à tous de dire ce que vous pensez ma formule.
Ne soyez pas surpris si je ne poste pas la formule elle-même: je ne sais pas encore quoi faire de ma formule encore.
Merci d'avance!
Silver.
Merci d'avoir répondu si tôt,
Mais concernant la formule, je veux être sûr qu'elle ne soit pas d'une grande utilité au niveau informatique avant de la divulguer: après tout, une nouvelle formule de conversion plus rapide que la méthode traditionnelle est quelque chose de grand.
En fait, ce que je demande surtout, c'est de savoir si une façon plus rapide pour convertir les bases est quelque chose de recherché... sinon, bien sûr que je vous la montrerais.
Mais concernant la formule, je veux être sûr qu'elle ne soit pas d'une grande utilité au niveau informatique avant de la divulguer: après tout, une nouvelle formule de conversion plus rapide que la méthode traditionnelle est quelque chose de grand.
En fait, ce que je demande surtout, c'est de savoir si une façon plus rapide pour convertir les bases est quelque chose de recherché... sinon, bien sûr que je vous la montrerais.
Donc c'est bien cette méthode qui est actuellement la plus rapide... maintenant je le sais, merci!
Cependant, la conversion par division successive, en un premier regard, semble comporter un nombre minimal d'opération: des divisions.
Or, à part si je me trompe, l'ordinateur fait ses divisions en soustrayant (par exemple: 10/2 c'est 10-2=8 -2=6 -2=4 -2=2 -2=0, donc 5 fois l'opération "-2".)
Ma formule est une suite d'additions: et j'ai vérifié; j'ai le même nombre d'addition pour une conversion donnée que le nombre de division pour la même conversion avec la méthode par division successive.
C'est pour cela que ma formule est plus rapide. Et inédite: je suis entré en contact avec un polytechnicien, et après lui avoir montré ma formule, il m'a dit qu'il n'avait jamais vu une conversion par addition successive.
Je pourrais me tromper, après tout, peut être que l'ordinateur effectue ses division autrement.
Cependant, la conversion par division successive, en un premier regard, semble comporter un nombre minimal d'opération: des divisions.
Or, à part si je me trompe, l'ordinateur fait ses divisions en soustrayant (par exemple: 10/2 c'est 10-2=8 -2=6 -2=4 -2=2 -2=0, donc 5 fois l'opération "-2".)
Ma formule est une suite d'additions: et j'ai vérifié; j'ai le même nombre d'addition pour une conversion donnée que le nombre de division pour la même conversion avec la méthode par division successive.
C'est pour cela que ma formule est plus rapide. Et inédite: je suis entré en contact avec un polytechnicien, et après lui avoir montré ma formule, il m'a dit qu'il n'avait jamais vu une conversion par addition successive.
Je pourrais me tromper, après tout, peut être que l'ordinateur effectue ses division autrement.
Je n'ai jamais entendu parlé d'une méthode par addition pour la conversion de base.
Un bon exemple d'algorithme de conversion de base correspond à la fonction itoa :
http://www.jb.man.ac.uk/~slowe/cpp/itoa.html
En effet un ordinateur effectue les divisions par une suite de soustraction / décalage de bit :
https://en.wikipedia.org/wiki/Division_algorithm
As-tu effectué des tests de temps d'execution sur des gros nombres entre la méthode actuelle et avec ta méthode ?
Un bon exemple d'algorithme de conversion de base correspond à la fonction itoa :
http://www.jb.man.ac.uk/~slowe/cpp/itoa.html
En effet un ordinateur effectue les divisions par une suite de soustraction / décalage de bit :
https://en.wikipedia.org/wiki/Division_algorithm
As-tu effectué des tests de temps d'execution sur des gros nombres entre la méthode actuelle et avec ta méthode ?
Donc, comme je ne peux pas (et n'ai pas trop envie) de détailler ma formule avant de la publier, je vais juste expliquer l'idée de ma formule (désoléééééé):
101 en base 3 est 10202.
Ma formule prend l'idée qu'il existe une suite d'addition tel que 101+X1+X2+X3+X4+X5=10202 (il y a 5 additions différentes tous déterminées par le coeur de ma formule, et chaque nombre à convertir possède un nombre d'addition différent, nombre d'addition qui est égal au nombre de chiffre du résultat final. Par exemple: 1020202020202 aurait 13 additions.)
Sans trop rentrer dans les détails, l'addition ressemble à:
101+231+770+2100+7000=10202
Désolé, je ne peux vraiment pas expliqué comment 231, 770, 2100 et 7000 s'impliquent dans ce calcul avant d'être absolument certains que ma formule ne peut pas être utilisé dans un programme pour rendre les calculs de l'ordinateur plus rapides.
101 en base 3 est 10202.
Ma formule prend l'idée qu'il existe une suite d'addition tel que 101+X1+X2+X3+X4+X5=10202 (il y a 5 additions différentes tous déterminées par le coeur de ma formule, et chaque nombre à convertir possède un nombre d'addition différent, nombre d'addition qui est égal au nombre de chiffre du résultat final. Par exemple: 1020202020202 aurait 13 additions.)
Sans trop rentrer dans les détails, l'addition ressemble à:
101+231+770+2100+7000=10202
Désolé, je ne peux vraiment pas expliqué comment 231, 770, 2100 et 7000 s'impliquent dans ce calcul avant d'être absolument certains que ma formule ne peut pas être utilisé dans un programme pour rendre les calculs de l'ordinateur plus rapides.
Le principe me paraît un peu bizarre car d'après ce que je comprends tu essayes de calculer X1, ..., X5 à partir de l'entrée (101) et de la sortie (10202).
J'ai sûrement mal compris le raisonnement que tu essayes d'expliquer. Mais sans avoir plus d'informations je ne vois pas ce que je peux faire de plus pour toi.
Je laisse quelqu'un de mieux placer pour peut-être t'aider mieux que je pourrais le faire.
Bon courage pour la suite.
J'ai sûrement mal compris le raisonnement que tu essayes d'expliquer. Mais sans avoir plus d'informations je ne vois pas ce que je peux faire de plus pour toi.
Je laisse quelqu'un de mieux placer pour peut-être t'aider mieux que je pourrais le faire.
Bon courage pour la suite.
ampholyte a écrit:Le principe me paraît un peu bizarre car d'après ce que je comprends tu essayes de calculer X1, ..., X5 à partir de l'entrée (101) et de la sortie (10202).
J'ai peut être oublié de mentionner qu'il est possible de calculer le nombre de chiffres que comporte le résultat rien qu'avec le nombre de départ.
D'ailleurs, je ne vois pas de mal à vous la montrer:
int(log10(x)*P)+1
x est le nombre de départ.
"int" c'est la partie entière.
P est un nombre qui varie selon la base et déterminée de façon expérimentale (je me suis pas encore penché sur P pour l'instant). Par exemple, pour la base 2, P=3.321... et pour la base 3, P=2.092...
Je n'ai pas encore calculé P pour le reste des bases (en fait je viens de le faire pour la base 3, je ne travaillais qu'avec la base 2 jusqu'à présent).
Donc voilà, j'espère que cela résout le problème.
Crystal Silver a écrit:J'ai peut être oublié de mentionner qu'il est possible de calculer le nombre de chiffres que comporte le résultat rien qu'avec le nombre de départ.
D'ailleurs, je ne vois pas de mal à vous la montrer:
int(log10(x)*P)+1
x est le nombre de départ.
"int" c'est la partie entière.
P est un nombre qui varie selon la base et déterminée de façon expérimentale (je me suis pas encore penché sur P pour l'instant). Par exemple, pour la base 2, P=3.321... et pour la base 3, P=2.092...
Je n'ai pas encore calculé P pour le reste des bases (en fait je viens de le faire pour la base 3, je ne travaillais qu'avec la base 2 jusqu'à présent).
Donc voilà, j'espère que cela résout le problème.
Le nombre de chiffre que comporte le résultat est une formule déjà connu :
si x est le nombre de départ et b la base d'arrivé alors int(log_b(x)) +1)
est le nombre de chiffre de l'écriture de x en base b où log_b est le logarithme en base b.
et il se trouve que log_b(x) = log10(x)/log10(b), donc ta variable P est égal à 1/log10(b).
salut
7 msg sur ce forum de math ....
une formule classique qui donne le nombre de chiffres d'un entier écrit en base b que tu ne comprends pas (que tu as trouvée c'est bien mais la comprendre c'est donner du sens aux objets mathématiques) et qui peux se comprendre dès qu'on connaît les logarithmes ....
la compréhension est immédiate lorsque qu'on sait que tout entier n appartient à un intervalle et la relation entre les différents logarithmes en différentes bases ....
et la relation entre les différents logarithmes en différentes bases ....
quel niveau/age as-tu ?
je ne pense pas que tu ait inventé grand chose ....
7 msg sur ce forum de math ....
une formule classique qui donne le nombre de chiffres d'un entier écrit en base b que tu ne comprends pas (que tu as trouvée c'est bien mais la comprendre c'est donner du sens aux objets mathématiques) et qui peux se comprendre dès qu'on connaît les logarithmes ....
la compréhension est immédiate lorsque qu'on sait que tout entier n appartient à un intervalle
quel niveau/age as-tu ?
je ne pense pas que tu ait inventé grand chose ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Une petite erreur de ma part mène donc à une image totalement différente que celle que je donnais...
Je dois par contre avouer que mes connaissances mathématiques ne sont pas très poussées, disons que j'apprend seul, d'où mes manques d'informations dans quelques domaines, notamment dans les logarithmes. Je suis plus un physicien que mathématicien.
De plus, le sujet de ce forum est "une nouvelle méthode pour convertir les bases par addition successive", méthode dont apparemment personne n'a jamais entendu parler de, et dont j'ai découvert en m'ennuyant.
Sinon, j'entre dans une CPGE, à Paris. Une bonne prépa, si je peux en dire autant. Mais ce n'est pas le sujet ici, n'est-ce pas?
L'information que je veux surtout obtenir, et pour cela j'ai déjà contacté l'académie des sciences, est la valeur intellectuelle et matérielle de cette nouvelle méthode par additions successives.
Je suis désolé pour avoir donné une mauvaise image de ma personne, et je ne souhaite surement pas que cette mauvaise image reste: il ne faut surtout pas que d'autres personnes ne me prennent pas au sérieux si je souhaite avoir une conversation avec eux.
Je dois par contre avouer que mes connaissances mathématiques ne sont pas très poussées, disons que j'apprend seul, d'où mes manques d'informations dans quelques domaines, notamment dans les logarithmes. Je suis plus un physicien que mathématicien.
De plus, le sujet de ce forum est "une nouvelle méthode pour convertir les bases par addition successive", méthode dont apparemment personne n'a jamais entendu parler de, et dont j'ai découvert en m'ennuyant.
Sinon, j'entre dans une CPGE, à Paris. Une bonne prépa, si je peux en dire autant. Mais ce n'est pas le sujet ici, n'est-ce pas?
L'information que je veux surtout obtenir, et pour cela j'ai déjà contacté l'académie des sciences, est la valeur intellectuelle et matérielle de cette nouvelle méthode par additions successives.
Je suis désolé pour avoir donné une mauvaise image de ma personne, et je ne souhaite surement pas que cette mauvaise image reste: il ne faut surtout pas que d'autres personnes ne me prennent pas au sérieux si je souhaite avoir une conversation avec eux.
Euh, je crois que tu t'emballe un peu là.
déjà qu'est ce que tu veux dire par addition successive ?
on doit pouvoir facilement trouver une formule c(n,k,b) qui donne le kième chiffre en base b de n.
et ensuite dire que n en base b est la somme de k=0 à (nb_chiffre n en base b) de c(n,k,b) * 10^k.
Est-ce pour toi une méthode par addition successive ?
et ta méthode est-elle vraiment par addition successive ?
i.e pour trouver tes nombre 231, 7000, 770, etc ds l'exemple que tu as donné, ne fais tu vraiment aucune division ni soustraction ?
3 + (-5) est-ce une addition ou une soustraction ? là parler d'addition ou soustraction est simplement jouer sur les mots
quand à la valeur intellectuelle d'une telle méthode, ça dépend, est-ce que tu utilise des idées nouvelles,
avec des méthode de démonstration nouvelle ? si c'est le cas alors oui.
Est ce que tu as juste une formule amusante qui converti ton nombre en base b, dont la preuve ce fait par des
manipulations arithmétique, raisonnement par récurrence, ou autre méthode de raisonnement connu ?
dans ce cas, non, ta formule n'a aucune valeur intellectuelle.
De plus apparemment tu as dit que ta formule ne fonctionnait que pour les base inférieur à 10 ce qui limite rapidement son intérêt.
Le seul intérêt à la rigueur qu'elle pourrait avoir, c'est en informatique, si c'est un algorithme plus efficaces que ceux
utiliser actuellement, mais une différence de quelque seconde sur des nombre aussi grand que 10^250 ou 10^350
ce n'est pas significatif :/
déjà qu'est ce que tu veux dire par addition successive ?
on doit pouvoir facilement trouver une formule c(n,k,b) qui donne le kième chiffre en base b de n.
et ensuite dire que n en base b est la somme de k=0 à (nb_chiffre n en base b) de c(n,k,b) * 10^k.
Est-ce pour toi une méthode par addition successive ?
et ta méthode est-elle vraiment par addition successive ?
i.e pour trouver tes nombre 231, 7000, 770, etc ds l'exemple que tu as donné, ne fais tu vraiment aucune division ni soustraction ?
3 + (-5) est-ce une addition ou une soustraction ? là parler d'addition ou soustraction est simplement jouer sur les mots
quand à la valeur intellectuelle d'une telle méthode, ça dépend, est-ce que tu utilise des idées nouvelles,
avec des méthode de démonstration nouvelle ? si c'est le cas alors oui.
Est ce que tu as juste une formule amusante qui converti ton nombre en base b, dont la preuve ce fait par des
manipulations arithmétique, raisonnement par récurrence, ou autre méthode de raisonnement connu ?
dans ce cas, non, ta formule n'a aucune valeur intellectuelle.
De plus apparemment tu as dit que ta formule ne fonctionnait que pour les base inférieur à 10 ce qui limite rapidement son intérêt.
Le seul intérêt à la rigueur qu'elle pourrait avoir, c'est en informatique, si c'est un algorithme plus efficaces que ceux
utiliser actuellement, mais une différence de quelque seconde sur des nombre aussi grand que 10^250 ou 10^350
ce n'est pas significatif :/
Merci pour enfin me dire l'utilité de ma formule. Et je reconnais m'être emballé un peu (beaucoup): après tout j'ai travaillé pendant quelques semaines sur cette formule.
Je pense que ma formule utilise des idées nouvelles, après tout, ceux à qui j'ai montré ma formule n'ont rien reconnu d'existant. Comme elle n'a aucune valeur matérielle, je veux qu'elle serve au moins d'une intrigue pour vous.
Voilà ma formule:
http://latex.codecogs.com/gif.latex?x+%5Csum_%7Bk%3D1%7D%5E%7Bint%28log_b%28x%29%29+1%7D%28int%28%5Cfrac%7Bx%7D%7Bb%5E%7Bk%7D%7D%29*%281-%5Cfrac%7Bb%7D%7B10%7D%29*10%5E%7Bk%7D%29
C'est un editeur de formule en ligne pour ceux qui ne connaissent pas (et pas un lien suspect). En forme de code, c'est (en language Python):
from math import log10
x= int(raw_input('Nombre de depart ' ))
z= int(raw_input('Base visee ' ))
j=0
for k in range(1, int((log10(x))/(log10(z))+1)):
***INDENTATION***j=j+int(x/(z**k))*(1.-(z/10.))*(10.**k)
y=int(x+j)
print y
C'est exactement ce que tu disais, bolza: le coeur de la formule est c(n,k,b) mis dans une boucle de 1 (pas 0) au nombre de chiffre de x en base b.
Sur le fait de trouver facilement de bout de formule, disons qu'il faut en avoir l'idée, ce n'est pas vraiment compliqué.
Je me suis juste amusé à développer cette formule, et je n'ai pas vraiment vérifié si le principe était déjà utilisé ou pas, sous cette forme ou une autre. Du moins personne ne m'a dit: "Hé! J'ai déjà vu cette méthode quelque part...".
Vous pourriez me dire ce que vous pensez de cette formule? Et aussi, si cette formule est nouvelle, peut-être m'aider à en faire un programme qui prendrais moins de temps à s'effectuer?
Je pense que ma formule utilise des idées nouvelles, après tout, ceux à qui j'ai montré ma formule n'ont rien reconnu d'existant. Comme elle n'a aucune valeur matérielle, je veux qu'elle serve au moins d'une intrigue pour vous.
Voilà ma formule:
http://latex.codecogs.com/gif.latex?x+%5Csum_%7Bk%3D1%7D%5E%7Bint%28log_b%28x%29%29+1%7D%28int%28%5Cfrac%7Bx%7D%7Bb%5E%7Bk%7D%7D%29*%281-%5Cfrac%7Bb%7D%7B10%7D%29*10%5E%7Bk%7D%29
C'est un editeur de formule en ligne pour ceux qui ne connaissent pas (et pas un lien suspect). En forme de code, c'est (en language Python):
from math import log10
x= int(raw_input('Nombre de depart ' ))
z= int(raw_input('Base visee ' ))
j=0
for k in range(1, int((log10(x))/(log10(z))+1)):
***INDENTATION***j=j+int(x/(z**k))*(1.-(z/10.))*(10.**k)
y=int(x+j)
print y
C'est exactement ce que tu disais, bolza: le coeur de la formule est c(n,k,b) mis dans une boucle de 1 (pas 0) au nombre de chiffre de x en base b.
Sur le fait de trouver facilement de bout de formule, disons qu'il faut en avoir l'idée, ce n'est pas vraiment compliqué.
Je me suis juste amusé à développer cette formule, et je n'ai pas vraiment vérifié si le principe était déjà utilisé ou pas, sous cette forme ou une autre. Du moins personne ne m'a dit: "Hé! J'ai déjà vu cette méthode quelque part...".
Vous pourriez me dire ce que vous pensez de cette formule? Et aussi, si cette formule est nouvelle, peut-être m'aider à en faire un programme qui prendrais moins de temps à s'effectuer?
Je suis plus que surpris que tu obtiennnes des meilleurs temps avec ce genre de formule.
Dans l'algorithme classique, on fait des divisions successives par b de nombre de plus en plus petit.
alors que dans ta formule tu fait des division par des puissances successives de b
(tu noteras que les deux méthodes font des divisions successives)
En gros pour utiliser ce genre de formule, il faut d'abord calculer, les puissance de b, ensuite diviser x
par ces puissances (sans parler des autre opération).
Alors qu'avec la méthode normale tu ne fait que des division par b.
Je ne sais pas avec quoi ni comment tu as comparer les temps, mais ta formule a une complexité plus grande que l'algorithme usuel :/
P.S: ce n'est pas cette formule là que j'avais en tête, mais plutôt celle-ci :
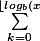}\rfloor+1}(\lfloor \dfrac{x}{b^k}\rfloor - \lfloor\dfrac{x}{b^{k+1}}\rfloor*b)*10^k)
formule tout aussi inefficace.
Si tout le monde te dis qu'il n'a jamais entendu parler d'une telle formule, c'est surtout parce que
ce genre de truc n'est pas enseigné, et ce n'est pas enseigné parce que c'est un truc que jamais
personne n'utilisera dans la pratique, et pas très intéressant théoriquement.
et puis convertir des nombres dans une autre base, à part pour les informaticiens avec les base 2 et 16
ou pour des "historiens des maths" qui découvre des documents de civilisations qui comptaient dans
des bases différentes, ça ne sert pas à grand chose, ça ne change en rien la propriété des nombres.
(en fait a peu près seules les critères de divisibilité changes, mais il est inutile de connaître les
critères de divisibilité des nombres écrit dans une base dans laquelle on ne calcule pas)
donc la seule chose enseigner sur les bases, ce sont seulement les truc "basiques" si je puis dire ^^
Demande au gens si ils ont déjà vu la formule que je t'ai donné, je pense tu aura la même réponse,
pourtant cette formule est certainement connue depuis longtemps. Elle repose simplement sur le
fait que en base b, une multiplication ou une division par b, consiste simplement en un décalage de
la virgule. Donc je te rassure, rien de nouveau là-dedans
Ceci dit c'est bien que tu l'ai retrouver (modulo associativité et bidouillage, c'est la même)
Dans l'algorithme classique, on fait des divisions successives par b de nombre de plus en plus petit.
alors que dans ta formule tu fait des division par des puissances successives de b
(tu noteras que les deux méthodes font des divisions successives)
En gros pour utiliser ce genre de formule, il faut d'abord calculer, les puissance de b, ensuite diviser x
par ces puissances (sans parler des autre opération).
Alors qu'avec la méthode normale tu ne fait que des division par b.
Je ne sais pas avec quoi ni comment tu as comparer les temps, mais ta formule a une complexité plus grande que l'algorithme usuel :/
P.S: ce n'est pas cette formule là que j'avais en tête, mais plutôt celle-ci :
formule tout aussi inefficace.
Si tout le monde te dis qu'il n'a jamais entendu parler d'une telle formule, c'est surtout parce que
ce genre de truc n'est pas enseigné, et ce n'est pas enseigné parce que c'est un truc que jamais
personne n'utilisera dans la pratique, et pas très intéressant théoriquement.
et puis convertir des nombres dans une autre base, à part pour les informaticiens avec les base 2 et 16
ou pour des "historiens des maths" qui découvre des documents de civilisations qui comptaient dans
des bases différentes, ça ne sert pas à grand chose, ça ne change en rien la propriété des nombres.
(en fait a peu près seules les critères de divisibilité changes, mais il est inutile de connaître les
critères de divisibilité des nombres écrit dans une base dans laquelle on ne calcule pas)
donc la seule chose enseigner sur les bases, ce sont seulement les truc "basiques" si je puis dire ^^
Demande au gens si ils ont déjà vu la formule que je t'ai donné, je pense tu aura la même réponse,
pourtant cette formule est certainement connue depuis longtemps. Elle repose simplement sur le
fait que en base b, une multiplication ou une division par b, consiste simplement en un décalage de
la virgule. Donc je te rassure, rien de nouveau là-dedans
Ceci dit c'est bien que tu l'ai retrouver (modulo associativité et bidouillage, c'est la même)
Dans une calculette, je verrais bien ça comme ça:
On tape un chiffre, le 7 par exemple, et il y a une transfo directe en binaire 111 par de la mémoire incrustée.
Si on tape 1 derrière pour faire 71:
le 111 est multiplié par 10, cad par 8+2, et là c'est facile et immédiat:
111000+1110=1000110 et on ajoute 1=1000111
Si on tape un 8 pour faire 718, on recommence.
Bref, immédiatement après avoir écrit un chiffre, le nombre binaire est déja en machine. C'est du temps transparent.
On tape un chiffre, le 7 par exemple, et il y a une transfo directe en binaire 111 par de la mémoire incrustée.
Si on tape 1 derrière pour faire 71:
le 111 est multiplié par 10, cad par 8+2, et là c'est facile et immédiat:
111000+1110=1000110 et on ajoute 1=1000111
Si on tape un 8 pour faire 718, on recommence.
Bref, immédiatement après avoir écrit un chiffre, le nombre binaire est déja en machine. C'est du temps transparent.
je pense que la calculette ne fait pas à proprement parler de conversion ^^
quand on appuie sur une touche, on ferme certaine partie d'un circuit, qui fait
que les bons signaux vont directement être envoyer à l'unité de calcul.
Elle va utiliser plutôt des truc comme des décodeurs par exemple.
Si par exemple, le résultat d'un calcul est 7, alors la suite 111
(qui est en fait un ensemble de signaux électrique) va être envoyer dans un décodeur
qui va dire : bah allume la led en haut, puit les deux led à droite, ce qui fait que nous
on va voir un 7 s'afficher, mais elle ne fera pas de conversion de 111 (en base 2) en 7 ^^
Après je ne sait pas précisément comment ça se passe, mais il est possible qu'il y ait un circuit
qui fasse l'opération "*10 + x" un peu comme tu le décrit pour les données que l'on entre.
quand on appuie sur une touche, on ferme certaine partie d'un circuit, qui fait
que les bons signaux vont directement être envoyer à l'unité de calcul.
Elle va utiliser plutôt des truc comme des décodeurs par exemple.
Si par exemple, le résultat d'un calcul est 7, alors la suite 111
(qui est en fait un ensemble de signaux électrique) va être envoyer dans un décodeur
qui va dire : bah allume la led en haut, puit les deux led à droite, ce qui fait que nous
on va voir un 7 s'afficher, mais elle ne fera pas de conversion de 111 (en base 2) en 7 ^^
Après je ne sait pas précisément comment ça se passe, mais il est possible qu'il y ait un circuit
qui fasse l'opération "*10 + x" un peu comme tu le décrit pour les données que l'on entre.
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
