Bonsoir et bonne lecture :
http://happy-arabia.net/Conjecture-de-Syracuse-Collatz.pdf
Cordialement
Ahmed Idrissi Bouyahyaoui
Conjecture de Syracuse (nouvelle approche)
8 messages
- Page 1 sur 1
AIB a écrit:Bonsoir et bonne lecture :
http://happy-arabia.net/Conjecture-de-Syracuse-Collatz.pdf
Cordialement
Ahmed Idrissi Bouyahyaoui
Je suis impatient de lire les commentaires des forumers de ce site!
j'ai un peu de mal à suivre le papier..
Ça se propose d'être une démonstration de la conjecture ?
C'est un peu brouillon. Par exemple à plusieurs reprises vous parlez du cycle 1-4-2-1. Ce cycle est obtenu avec l'autre variante de la suite de Syracuse :
Bon, pour moi ça ne tient pas.
Pour le peu que j'ai compris, on met en évidence une impossiblité que le plus petit nombre d'une éventuelle boucle soit le plus petit. Si c'est en partie vrai (ce n'est pas toujours le cas) ça n'empêche absolument pas la possibilité de la boucle: Un nombre plus petit que le plus petit de la boucle peut y accéder sans en faire partie.
Il faut mettre de coté la voie de la logique de base pour cette conjecture. La possibilité de boucle est réelle. Peu probable, mais réelle.
Pour le peu que j'ai compris, on met en évidence une impossiblité que le plus petit nombre d'une éventuelle boucle soit le plus petit. Si c'est en partie vrai (ce n'est pas toujours le cas) ça n'empêche absolument pas la possibilité de la boucle: Un nombre plus petit que le plus petit de la boucle peut y accéder sans en faire partie.
Il faut mettre de coté la voie de la logique de base pour cette conjecture. La possibilité de boucle est réelle. Peu probable, mais réelle.
Bonsoir,
le problème de la majoration est indécidable.
Soit la suite de Syracuse {Mi} majorante, à priori, de toute suite de Collatz {Ni} avec i=0, 1, 2, . , j .
Sil existe toujours un j supérieur à n alors le problème de la majoration de la suite de Collatz {Ni} par la suite de Syracuse {Mi} est indécidable du moins pour cette approche.
Létablissement de lunicité du cycle trivial pour les suites de Collatz bornées demeure valide.
le problème de la majoration est indécidable.
Soit la suite de Syracuse {Mi} majorante, à priori, de toute suite de Collatz {Ni} avec i=0, 1, 2, . , j .
Sil existe toujours un j supérieur à n alors le problème de la majoration de la suite de Collatz {Ni} par la suite de Syracuse {Mi} est indécidable du moins pour cette approche.
Létablissement de lunicité du cycle trivial pour les suites de Collatz bornées demeure valide.
Bonjour,
Je donne des précisions qui améliorent la compréhension de larticle :
La suite_ n) de premier élément
de premier élément  avec
avec /3^n) est une suite de Syracuse et, par suite, elle est bornée pour tout n.
est une suite de Syracuse et, par suite, elle est bornée pour tout n.
La suite de Syracuse _n) de premier élément
de premier élément  , où n est un entier positif aussi grand quon le veut et
, où n est un entier positif aussi grand quon le veut et /3^n) , est un majorant de « laltitude » de toute suite {
, est un majorant de « laltitude » de toute suite {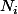 } construite suivant lalgorithme de Collatz (suite de Collatz) avec i=0, 1, 2,
. , j.
} construite suivant lalgorithme de Collatz (suite de Collatz) avec i=0, 1, 2,
. , j.
Sil existe toujours un j supérieur à tout n alors n ne peut être un majorant de la « longitude » j de la suite {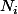 } bornée en « altitude » car les éléments
} bornée en « altitude » car les éléments  appartiennent alors à un cycle et j peut être aussi grand quon le veut.
appartiennent alors à un cycle et j peut être aussi grand quon le veut.
http://happy-arabia.net/Conjecture-de-Syracuse-Collatz.pdf
Cordialement
Ahmed Idrissi Bouyahyaoui
Je donne des précisions qui améliorent la compréhension de larticle :
La suite
La suite de Syracuse
Sil existe toujours un j supérieur à tout n alors n ne peut être un majorant de la « longitude » j de la suite {
http://happy-arabia.net/Conjecture-de-Syracuse-Collatz.pdf
Cordialement
Ahmed Idrissi Bouyahyaoui
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
