Je ne tiens pas à polémiquer, mais plutôt à faire une synthèse du problème.
Première remarque:ça fait plus de 35 ans que je suis professeur agrégé de mathématiques et je n'ai jamais vu une construction de l'exponentielle comme
)
Il y a déjà un bout de temps on définissait
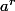
, avec

réel>0 et

comme

. il fallait de nombreuses heures pour vérifier toutes les propriétés des exposants, mais si 2 fonctions continues coïncident sur une partie dense de R comme Q elles sont égales sur R et on avait nos exponentielles.
On posait
)=\lim_{r\to oo}(\frac{a^r-1}{r}))
et l'exponentielle naturelle était celle qui vérifiait
'=1)
Tout cela se faisait il y a 40 ans en Sup et ça plus la construction de R, c'était à vous dégoûter de maths.
Une autre possibilité consistait à définir ln avant exp comme pour x>0,
=\bigint_{1}^{x}\frac{dx}{x})
;
Mais tout repose, F étant une primitive de

sur
=\bigint_{1}^{x}\frac{dx}{x}=F(x)-F(1))
et ce résultat, tu ne l'a pas démontré, vu qu'il repose sur l'uniforme continuité qui ne se voit pas en première année!
Reste, ce qui se fait actuellement en spé:
Soit la série entière:

, cette série, qui (qui est aussi une suite) n'est autre que le développement limité de l'exponentielle prolongé infiniment, a un rayon de convergence infinie, donc est convergente pour tout z et on peut écrire:
=\bigsum_{k=0}^{k=oo}\frac{z^k}{k!})
et sur tout compact de R, elle est uniformément ce qui permet de faire ce que l'on veut:
Elle est continue, car chaque somme partielle l'est;
Elle est dérivable et on peut dériver terme à terme, d'où
)'=exp(x))
avec
0 =1.)
De plus, on a
.exp(y)=(\bigsum_{k=0}^{k=oo}\frac{x^k}{k!})(\bigsum_{k=0}^{k=oo}\frac{y^k}{k!})=\bigsum_{k=0}^{k=oo}\bigsum_{h=0}^{h=oo}=)
^k}{k!})
=exp(x+y)
et ensuite on montre que
et
sont adjacentes. Du coup un théorème nous permet de conclure que
converge.
