J'ai beaucoup de mal à comprendre les applications sur les e

[skyskiper]

Salut à tous!
Voilà, j'ai de grosse de difficultés à résoudre les exercices où il est question d'applications sur des ensembles et j'aimerai avoir quelques précisions:
On pose E et F deux ensembles et f une application de E dans F. Soi A un sous ensembles de E.
Est-ce que:
-> ?
-> ?
Merci à tous ceux qui prendront le temps de me répondre! (je suis vraiment désespéré... :triste: )

[tize]

Non pour la première (regarder par exemple des fonctions non injectives)
Oui pour la deuxième, en général tout marche bien avec les fonctions réciproques... mais attention à écrire plutôt

[yos]

Pour le premier, prend E=F=R , A=R+ et f(x)=x².
Qui est f(A)? et f(-3) est-il dans f(A)? et -3 est-il dans A?

[skyskiper]

Donc si j'ai bien compris le raisonnement, je peux dire que:

C'est bien ça?
Merci

[Imod]

Si f est une fonction , la notation f(x) ne pose pas de problème , au pire f(x) n'existe pas mais elle ne peut en aucun cas prendre deux valeurs . Par contre pose problème car c'est un ensemble éventuellement vide qui peut contenir plusieurs éléments . Avec cette précaution , on peut quand même écrire :

.

Imod

[abcd22]

Bonsoir,
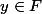
Pour être vraiment rigoureux on devrait écrire () pour désigner , et réserver la notation au cas où f est bijective et admet une application réciproque .

Rq : tu dis que A est un sous-ensemble de E, donc tu ne peux pas parler de , on peut seulement parler de (l'ensemble des éléments de E qui sont envoyés dans B par f) pour B sous-ensemble de F.