BiancoAngelo a écrit:Salut !
J'ai cherché il y a quelques temps si vraiment on avait besoin de la continuité, car j'en parlais à une de mes élèves de Terminale. En l'occurrence, je ne me suis pas convaincu que c'était vital. En fait, il semble que l'hypothèse de convergence et de continuité soient très liées.
Bref.
Si jamais on suppose que
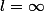
, f(l) a donc pour sens
)
qui serait donc infini...
La question est de savoir si on considère l'infini comme un point fixe. C'est un peu louche !
De même, si la limite est pas dans l'intervalle, c'est qu'il n'y a pas de point fixe... sur l'intervalle ! Donc pour les ouverts où la limite est sur le bord, c'est foutu...
Mais c'est un peu du n'importe quoi si on considère qu'il suffit juste de le fermer (dans le cas où la limite est finie) pour rendre tout ça valable.
Ces questions sont fondées, mais au final, on tourne en rond je trouve.
La continuité est indispensable. Je suis catégorique.
Dans le cours de mon prof I est fermé, ce qui évite la deuxième question questions. Mais il n'est pas borné, ce qui m'a amené à m'interroger, consulter le site de M. Costantini, et me poser encore plus de questions :marteau:
En ce qui concerne le cours de mon prof, je suppose que quand il écrit "
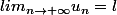
", il entends "la suite est convergente de limite l", et donc que l est réel (mais la notation laisse un peu planer le doute). J'attends que son poly soit en ligne pour me faire les dents.
Le fait que si u_n tend vers +l'infini alors f tends vers +l'infini me semble intuitivement juste mais reste à prouver. Et non, l'infini n'est pas un point fixe de f

BREF j'ai mal lu, dans le poly de M. Costantini a bien indiqué
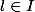
, donc je vais me flageller avec des orties fraiches.
ps : je ne vois pas trop en quoi "fermer l'intervalle" serait une entourloupe, c'est très courant comme restriction (une fonction continue sur un intervalle fermé borné est bornée ; si l'intervalle n'est pas fermé, cela devient faux en général)
