égalité de deux fonctions

[MC91]

Bonjour,

Nous avons corrigé un exercice en cours et il y a une partie que je ne comprends pas.
Nous obtenons à un moment f(t)= g(t) pour tout t dans [0,1] (f et g sont deux fonctions continues sur [0,1])
On en conclut directement que f=g.

Je ne comprend pas pourquoi f=g. Cela signifie que pour n'importe quel t réel, on aurait f(t)=g(t)?

Merci pour vos réponses.
Bonne journée

[zaidoun]

Bien sur oui. En chaque point de l'intervalle [0, 1] on a l'égalité, par conséquent f=g.

[MC91]

Bien sur oui. En chaque point de l'intervalle [0, 1] on a l'égalité, par conséquent f=g.

Cela veut dire que par exemple, pour t=2, on a f(2)=g(2)?
Je ne comprend pas pourquoi la condition f(t)=g(t) sur [0,1] permet de généraliser en disant que f(t)=g(t) pour tout réel t

[zygomatique]

salut

pour être précis se donner une fonction f c'est se donner une opération (l'expression de f) et son domaine de définition ...

dans ce cas si et sont deux fonctions alors





évidemment (1) est une condition nécessaire et (2) une condition suffisante ....

ainsi par exemple les fonctions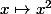 définies respectivement sur et sur ne sont pas égales ....


:lol3:

[dlzlogic2]

Bonjour,
Exemple ou contre-exemple ?
f(x)=x
g(x)= abs(x)
Pour tout t appartenant à [0;1] f(t) = g(t).
f et g sont continues et égales sur [0;1].
Peut-on dire que f=g ?

[MC91]

Bonjour,
Exemple ou contre-exemple ?
f(x)=x
g(x)= abs(x)
Pour tout t appartenant à [0;1] f(t) = g(t).
f et g sont continues et égales sur [0;1].
Peut-on dire que f=g ?

Pour moi non, puisque lorsqu'on prend t=-2 par exemple, f(-2) n'est pas égal à g(-2)

[Skullkid]

Relire ce qu'a dit zygomatique : le domaine de définition (on dira plutôt son ensemble de départ, en l'occurrence) fait partie de la définition d'une fonction.

Quand l'énoncé de ton exercice dit "soit f une fonction continue sur [0,1]", ça veut dire, sauf indication contraire, que f n'est définie que sur [0,1]. Donc f(2) n'a aucun sens. En l'occurrence, comme tes deux fonctions f et g ne sont définies que sur [0,1], l'égalité "f(x) = g(x) pour tout x de [0,1]" entraîne l'égalité f = g.

J'insiste encore : on peut très bien définir la fonction . Avec cette définition, f(2) n'a aucun sens, même si |2| a un sens. De plus, f est égale à la fonction

[Doraki]

Chez moi l'ensemble d'arrivée fait aussi partie de la définition d'une fonction.
(mais bon j'imagine que vos fonctions sont implicitement déclarées à valeurs dans R)

[Skullkid]

Chez moi l'ensemble d'arrivée fait aussi partie de la définition d'une fonction.

Absolument, très important quand on a affaire à des problèmes d'injectivité/surjectivité.

[zygomatique]

Chez moi l'ensemble d'arrivée fait aussi partie de la définition d'une fonction.
(mais bon j'imagine que vos fonctions sont implicitement déclarées à valeurs dans R)

certes oui ...

mais pour arriver quelque part ... faut déjà partir de quelque part !!!!

:ptdr: