Optimisation de fonction
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
camilia89
- Membre Naturel
- Messages: 12
- Enregistré le: 11 Déc 2014, 15:07
-
 par camilia89 » 12 Déc 2014, 13:48
par camilia89 » 12 Déc 2014, 13:48
Cliffe a écrit:ah bon ?
Fait l'application numérique pour

et
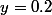
ou encore pour

et

.
Oui vous avez raison, je vais revoir ça ...
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 12 Déc 2014, 13:51
par Cliffe » 12 Déc 2014, 13:51
camilia89 a écrit:Oui vous avez raison, je vais revoir ça ...
Maintenant essaye :
 = x^\beta-ay^\beta)
.
-
camilia89
- Membre Naturel
- Messages: 12
- Enregistré le: 11 Déc 2014, 15:07
-
 par camilia89 » 16 Déc 2014, 15:27
par camilia89 » 16 Déc 2014, 15:27
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 16 Déc 2014, 16:53
par Cliffe » 16 Déc 2014, 16:53
Pas très rigoureux mais ça doit être juste (pas tout vérifier).
Pour la formule complète, il vaut mieux approximer la valeur optimale que de chercher une formule générale.
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 16 Déc 2014, 21:07
par Cliffe » 16 Déc 2014, 21:07
[CENTER]
 = x^\beta-ay^\beta \ \ \ \ \beta \in ]0,1] \ \ \ \ (x,y,a) \in [0,1]^3)
[/CENTER]
cas 1 : 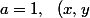 \in [0,1]^2)
[CENTER]
 = x^\beta-y^\beta)
cas déjà traiter.[/CENTER]
cas 2 : 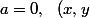 \in [0,1]^2)
[CENTER]
 = x^\beta)
cas déjà traiter.[/CENTER]
cas 3 : 
_____
cas 3.1 : 
[CENTER]
 = (1-a) x^\beta \Rightarrow \begin{array}{|c|} \hline \underset{a \in ]0, 1[, \ \ (x,y) \in ]0,1[^2, \ \ x = y}{\underset{\beta \in ]0, 1]}{argmax}} \left ( f_{x-ay} \left ( \beta \right ) \right ) = 0^+\\ \hline \end{array})
[/CENTER]
_____
cas 3.2 :  \in ]0,1[^2, \ \ x \ne y)
[CENTER]
 = x^\beta ln (x) - a y^\beta ln (y))
[/CENTER]
Soit

tel que
 = 0)
. Par le calcul, on obtient :
[CENTER]
}{ln \left ( x \right )} \right )}{ln \left ( x \right ) - ln \left ( y \right )})
[/CENTER]
__________
cas 3.2.1 : 
[CENTER]
 \right ) = 0^+ \\ \hline \end{array})
[/CENTER]
__________
cas 3.2.3 : 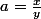
[CENTER]


On a donc :
 \in ]0,1[^2, \ \ x \ne y, \ \ a = \frac{x}{y}}{\underset{\beta \in ]0, 1]}{argmax}} \left ( f_{x-ay} \left ( \beta \right ) \right ) = 0^+ \\ \hline \end{array})
[/CENTER]
_____
cas 3.3 : 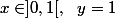
[CENTER]
=x^\beta-a\Rightarrow \begin{array}{|c|} \hline \underset{a \in ]0,1[, \ \ x \in ]0,1[, \ \ y = 1}{\underset{\beta \in ]0, 1]}{argmax}} \left ( f_{x-ay} \left ( \beta \right ) \right ) = 0^+\\ \hline \end{array})
[/CENTER]
_____
cas 3.4 : 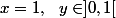
[CENTER]
=1-ay^\beta\Rightarrow \begin{array}{|c|} \hline \underset{a \in ]0,1[, \ \ x = 1, \ \ y \in ]0,1[}{\underset{\beta \in ]0, 1]}{argmax}} \left ( f_{x-ay} \left ( \beta \right ) \right ) = 1\\ \hline \end{array})
[/CENTER]
_____
cas 3.5 :  = (0,1))
[CENTER]
=-a\Rightarrow \begin{array}{|c|} \hline \underset{a \in ]0,1[, \ \ (x,y) = (0,1)}{\underset{\beta \in ]0, 1]}{argmax}} \left ( f_{x-ay} \left ( \beta \right ) \right ) = ]0,1]\\ \hline \end{array})
[/CENTER]
_____
cas 3.6 :  = (1,0))
[CENTER]
=1)
cas déjà traiter.[/CENTER]
_____
cas 3.7 : 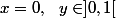
[CENTER]
=-ay^\beta\Rightarrow \begin{array}{|c|} \hline \underset{a \in ]0,1[, \ \ x = 0, \ \ y \in ]0,1[}{\underset{\beta \in ]0, 1]}{argmax}} \left ( f_{x-ay} \left ( \beta \right ) \right ) = 1\\ \hline \end{array})
[/CENTER]
_____
cas 3.8 : 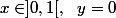
[CENTER]
=x^\beta)
cas déjà traiter.[/CENTER]
Et maintenant il reste à étudier :
z}(\beta)=g(\beta)=x^\beta-ay^\beta-(1-a)z^\beta)
-
camilia89
- Membre Naturel
- Messages: 12
- Enregistré le: 11 Déc 2014, 15:07
-
 par camilia89 » 17 Déc 2014, 11:33
par camilia89 » 17 Déc 2014, 11:33
D'après ces études il paraît qu'il y a une solution exacte !! j'ai essayé de remplacer les valeurs de x,y,z et a dans la dérivé et chercher la valeur de

qui l'annule mais la solution présentée est erronée (il me donne un nombre complexe) !!!
-
camilia89
- Membre Naturel
- Messages: 12
- Enregistré le: 11 Déc 2014, 15:07
-
 par camilia89 » 17 Déc 2014, 11:36
par camilia89 » 17 Déc 2014, 11:36
Est ce qu'on ne peut pas isoler

par l'intégration du log?
-
camilia89
- Membre Naturel
- Messages: 12
- Enregistré le: 11 Déc 2014, 15:07
-
 par camilia89 » 17 Déc 2014, 11:44
par camilia89 » 17 Déc 2014, 11:44
Cliffe a écrit:[CENTER]
 = x^\beta-ay^\beta \ \ \ \ \beta \in ]0,1] \ \ \ \ (x,y,a) \in [0,1]^3)
[/CENTER]
cas 1 : 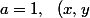 \in [0,1]^2)
[CENTER]
 = x^\beta-y^\beta)
cas déjà traiter.[/CENTER]
cas 2 : 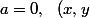 \in [0,1]^2)
[CENTER]
 = x^\beta)
cas déjà traiter.[/CENTER]
cas 3 : 
_____
cas 3.1 : 
[CENTER]
 = (1-a) x^\beta \Rightarrow \begin{array}{|c|} \hline \underset{a \in ]0, 1[, \ \ (x,y) \in ]0,1[^2, \ \ x = y}{\underset{\beta \in ]0, 1]}{argmax}} \left ( f_{x-ay} \left ( \beta \right ) \right ) = 0^+\\ \hline \end{array})
[/CENTER]
_____
cas 3.2 :  \in ]0,1[^2, \ \ x \ne y)
[CENTER]
 = x^\beta ln (x) - a y^\beta ln (y))
[/CENTER]
Soit

tel que
 = 0)
. Par le calcul, on obtient :
[CENTER]
}{ln \left ( x \right )} \right )}{ln \left ( x \right ) - ln \left ( y \right )})
[/CENTER]
__________
cas 3.2.1 : 
[CENTER]
 \right ) = 0^+ \\ \hline \end{array})
[/CENTER]
__________
cas 3.2.3 : 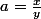
[CENTER]


On a donc :
 \in ]0,1[^2, \ \ x \ne y, \ \ a = \frac{x}{y}}{\underset{\beta \in ]0, 1]}{argmax}} \left ( f_{x-ay} \left ( \beta \right ) \right ) = 0^+ \\ \hline \end{array})
[/CENTER]
_____
cas 3.3 : 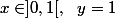
[CENTER]
=x^\beta-a\Rightarrow \begin{array}{|c|} \hline \underset{a \in ]0,1[, \ \ x \in ]0,1[, \ \ y = 1}{\underset{\beta \in ]0, 1]}{argmax}} \left ( f_{x-ay} \left ( \beta \right ) \right ) = 0^+\\ \hline \end{array})
[/CENTER]
_____
cas 3.4 : 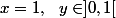
[CENTER]
=1-ay^\beta\Rightarrow \begin{array}{|c|} \hline \underset{a \in ]0,1[, \ \ x = 1, \ \ y \in ]0,1[}{\underset{\beta \in ]0, 1]}{argmax}} \left ( f_{x-ay} \left ( \beta \right ) \right ) = 1\\ \hline \end{array})
[/CENTER]
_____
cas 3.5 :  = (0,1))
[CENTER]
=-a\Rightarrow \begin{array}{|c|} \hline \underset{a \in ]0,1[, \ \ (x,y) = (0,1)}{\underset{\beta \in ]0, 1]}{argmax}} \left ( f_{x-ay} \left ( \beta \right ) \right ) = ]0,1]\\ \hline \end{array})
[/CENTER]
_____
cas 3.6 :  = (1,0))
[CENTER]
=1)
cas déjà traiter.[/CENTER]
_____
cas 3.7 : 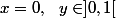
[CENTER]
=-ay^\beta\Rightarrow \begin{array}{|c|} \hline \underset{a \in ]0,1[, \ \ x = 0, \ \ y \in ]0,1[}{\underset{\beta \in ]0, 1]}{argmax}} \left ( f_{x-ay} \left ( \beta \right ) \right ) = 1\\ \hline \end{array})
[/CENTER]
_____
cas 3.8 : 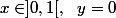
[CENTER]
=x^\beta)
cas déjà traiter.[/CENTER]
Et maintenant il reste à étudier :
z}(\beta)=g(\beta)=x^\beta-ay^\beta-(1-a)z^\beta)
merci bien Cliffe pour la correction de l'étude mais je crois pas que ça peut nous aider à résoudre la fonction de début!! :mur:
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 17 Déc 2014, 17:37
par Cliffe » 17 Déc 2014, 17:37
camilia89 a écrit:merci bien Cliffe pour la correction de l'étude mais je crois pas que ça peut nous aider à résoudre la fonction de début!! :mur:
Tu peux déjà calculer la dérivée et voir pour quel cas elle s'annule 0, 1 ou 2 fois.
-
camilia89
- Membre Naturel
- Messages: 12
- Enregistré le: 11 Déc 2014, 15:07
-
 par camilia89 » 17 Déc 2014, 17:59
par camilia89 » 17 Déc 2014, 17:59
Cliffe a écrit:Tu peux déjà calculer la dérivée et voir pour quel cas elle s'annule 0, 1 ou 2 fois.
Oui c'est ce que j'ai fait avant de poster ma question sur le forum, mais voici le résultat obtenu :
+y^{_Z}*ln(y)*a+z^{_Z}*ln(z)-z^{_Z}*ln(z)*a))
!!! c'est pas une chose calculable a priori car Z est une variable système que je connais pas sa valeur
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 17 Déc 2014, 19:25
par Cliffe » 17 Déc 2014, 19:25
Il faut une étude sur la dérivée maintenant. Tous les cas possibles (comme pour les fonctions d'avant).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 84 invités
et
ou encore pour
et
.

[/CENTER]
 = x^\beta-y^\beta)
 = x^\beta)
[/CENTER]
[/CENTER]
tel que
. Par le calcul, on obtient :
[/CENTER]
[/CENTER]

[/CENTER]
[/CENTER]
[/CENTER]
[/CENTER]
[/CENTER]