Optimisation de fonction
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
HERCOLUBUS
- Membre Relatif
- Messages: 105
- Enregistré le: 15 Nov 2011, 22:43
-
 par HERCOLUBUS » 24 Mai 2014, 19:30
par HERCOLUBUS » 24 Mai 2014, 19:30
Bonjour à tous!
Voici un numéro qui m'a mêlé :

Je dérive 2 fois, obtient

et

Je trouve 0 2 et 4 comme nombres critiques. Je trouve un maximum à m=4 et non pas à m=2 comme indique mon corrigé.
Est-ce que je suis distrait ou c'est juste?
Merci
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 24 Mai 2014, 19:49
par Cliffe » 24 Mai 2014, 19:49
Il résout 4 - 2 m = 0 apparemment.
-
HERCOLUBUS
- Membre Relatif
- Messages: 105
- Enregistré le: 15 Nov 2011, 22:43
-
 par HERCOLUBUS » 24 Mai 2014, 19:54
par HERCOLUBUS » 24 Mai 2014, 19:54
Cliffe a écrit:Il résout 4 - 2 m = 0 apparemment.
Donc la dose est bien 4 mg ?
Le test de la dérivée seconde sert à savoir si c'est un maximum ou un minimum, c'est bien ça?
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 24 Mai 2014, 20:03
par Cliffe » 24 Mai 2014, 20:03
Tu cherche le maximum de sensibilité. Donc le maximum de la fonction :
[CENTER]
 = \frac{dr(m)}{dm} = m(4-m))
[/CENTER]
Pour trouver le maximum, tu regarde ou la dérivée s'annule. Elle s'annule pour
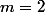
.
-
HERCOLUBUS
- Membre Relatif
- Messages: 105
- Enregistré le: 15 Nov 2011, 22:43
-
 par HERCOLUBUS » 24 Mai 2014, 20:48
par HERCOLUBUS » 24 Mai 2014, 20:48
Cliffe a écrit:Tu cherche le maximum de sensibilité. Donc le maximum de la fonction :
[CENTER]
 = \frac{dr(m)}{dm} = m(4-m))
[/CENTER]
Pour trouver le maximum, tu regarde ou la dérivée s'annule. Elle s'annule pour
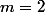
.
Ahh alors en fait j'ai mal considéré la question.
Je dois trouver la dérivée de la formule donnée, et ensuite faire le test de dérivée premièere et seconde à partir de cette dernière.
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 24 Mai 2014, 20:58
par Cliffe » 24 Mai 2014, 20:58
Y'a pas de dérivée seconde pour savoir si c'est un mini ou maxi, oublie ça. Tu regarde juste l'expression de la fonction pour voir qu'elle n'admet qu'un seul maximum.
Si tu veux vraiment faire la dérivée seconde, tu obtiens :
}{dm^2}=\frac{d^3r(m)}{dm^3}=-2<0)
donc s est concave, donc on a bien un maxi.
-
HERCOLUBUS
- Membre Relatif
- Messages: 105
- Enregistré le: 15 Nov 2011, 22:43
-
 par HERCOLUBUS » 24 Mai 2014, 21:58
par HERCOLUBUS » 24 Mai 2014, 21:58
Merci pour les précisions !!
-
camilia89
- Membre Naturel
- Messages: 12
- Enregistré le: 11 Déc 2014, 15:07
-
 par camilia89 » 11 Déc 2014, 15:27
par camilia89 » 11 Déc 2014, 15:27
Bonjour tout le monde,
j'ai une fonction g(beta) admettant beta comme variable et (x,y,z,a) sont des paramètres définis dans mon algorithme. Mon objectif est de chercher la valeur de beta qui maximise la fonction g. En simplifiant un peu la fonction g, elle s'écrit comme suit :
g(beta)=x^beta-(a*y^beta)-((1-a)*z^beta)
je veux chercher une formule de beta en fonction de x,y,z et a, à partir de laquelle je peux calculer la valeur de beta qui maximise cette fonction. Comment je peux faire ça?
SVP j'ai besoin de votre aide, s'il ya quelqu'un qui peut m'aider dans ce propos je serais reconnaissante.
Mercii d'avance
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 11 Déc 2014, 15:47
par Cliffe » 11 Déc 2014, 15:47
tu as des contraintes sur (x, y, z, a) ?
et un intervalle pour beta ?
-
camilia89
- Membre Naturel
- Messages: 12
- Enregistré le: 11 Déc 2014, 15:07
-
 par camilia89 » 11 Déc 2014, 15:59
par camilia89 » 11 Déc 2014, 15:59
Cliffe a écrit:tu as des contraintes sur (x, y, z, a) ?
et un intervalle pour beta ?
oui Cliffe, beta appartient à l'intervalle ]0,1], a propos x,y,z et a ce sont des paramètres appartenant à [0,1]. Dans mon algo itératif, à chaque itération je peux connaitre ces paramètres, reste à trouver la meilleur valeur de beta (maximisant g) en connaissant les param x,y,z et a.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Déc 2014, 16:20
par Ben314 » 11 Déc 2014, 16:20
Salut,
Tu as pas le signe de a ? celui de 1-a ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
camilia89
- Membre Naturel
- Messages: 12
- Enregistré le: 11 Déc 2014, 15:07
-
 par camilia89 » 11 Déc 2014, 16:30
par camilia89 » 11 Déc 2014, 16:30
"a" appartient aussi à [0,1] donc a et 1-a sont positifs
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 11 Déc 2014, 17:08
par Cliffe » 11 Déc 2014, 17:08
camilia89 a écrit:oui Cliffe, beta appartient à l'intervalle ]0,1], a propos x,y,z et a ce sont des paramètres appartenant à [0,1]. Dans mon algo itératif, à chaque itération je peux connaitre ces paramètres, reste à trouver la meilleur valeur de beta (maximisant g) en connaissant les param x,y,z et a.
Il faut prendre en compte tous les cas. Tu n'obtiendras pas une formule simple.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Déc 2014, 17:09
par Ben314 » 11 Déc 2014, 17:09
La dérivée de
))
est
t^\beta)
Donc, si
=x^\beta-ay^\beta-(1-a)z^\beta\)
alors
=\ln(x)x^\beta-a\ln(y)y^\beta-(1-a)\ln(z)z^\beta)
Donc
>0\ \Leftrightarrow\ h(\beta):=-a\ln(y)\big(\frac{y}{x}\big)^\beta-(1-a)\ln(z)\big(\frac{z}{x}\big)^\beta>-\ln(x))
Ce n'est pas une inéquation que l'on peut résoudre "formellement", mais on peut la résoudre numériquement a condition d'avoir une petite idée du comportement de la fonction

ce qui conduit naturellement... à la dériver...
Sauf qu'il va apparaitre du
)
et du
)
dont on ne connait a priori pas les signes d'où... étude de cas fastidieuse....
SAUF si tu connait dans quel ordre sont les réels x,y et z...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
camilia89
- Membre Naturel
- Messages: 12
- Enregistré le: 11 Déc 2014, 15:07
-
 par camilia89 » 11 Déc 2014, 21:19
par camilia89 » 11 Déc 2014, 21:19
Ben314 a écrit:La dérivée de
))
est
t^\beta)
Donc, si
=x^\beta-ay^\beta-(1-a)z^\beta\)
alors
=\ln(x)x^\beta-a\ln(y)y^\beta-(1-a)\ln(z)z^\beta)
Donc
>0\ \Leftrightarrow\ h(\beta):=-a\ln(y)\big(\frac{y}{x}\big)^\beta-(1-a)\ln(z)\big(\frac{z}{x}\big)^\beta>-\ln(x))
Ce n'est pas une inéquation que l'on peut résoudre "formellement", mais on peut la résoudre numériquement a condition d'avoir une petite idée du comportement de la fonction

ce qui conduit naturellement... à la dériver...
Sauf qu'il va apparaitre du
)
et du
)
dont on ne connait a priori pas les signes d'où... étude de cas fastidieuse....
SAUF si tu connait dans quel ordre sont les réels x,y et z...
p,p1,p2 et w sont des probabilités donc appartenant à [0,1]
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 11 Déc 2014, 21:39
par Cliffe » 11 Déc 2014, 21:39
Tu dois étudier la fonction suivant tous les cas possibles. Essaye déjà d'étudier :
[CENTER]
 = x^\beta-y^\beta \ \ \ \ \beta \in ]0,1] \ \ \ \ (x,y) \in [0,1]^2)
[/CENTER]
-
camilia89
- Membre Naturel
- Messages: 12
- Enregistré le: 11 Déc 2014, 15:07
-
 par camilia89 » 12 Déc 2014, 12:27
par camilia89 » 12 Déc 2014, 12:27
Cliffe a écrit:Tu dois étudier la fonction suivant tous les cas possibles. Essaye déjà d'étudier :
[CENTER]
 = x^\beta-y^\beta \ \ \ \ \beta \in ]0,1] \ \ \ \ (x,y) \in ]0,1]^2)
[/CENTER]
Bonjour Cliffe,
La dérivée de
 = f_{x-y}'= x^\beta-y^\beta)
est égal à
 - y^\beta*ln(y))

ssi
}{ln(y)})}{ln(x)-ln(y)})
alors :
1er cas :si
-ln(y) ln(\frac{ln(x)}{ln(y)})y -> ln(x)-ln(y) >0)
et
}{ln(y)}>1 => ln(\frac{ln(x)}{ln(y)})>0)
d'où

3e cas si x=y alors
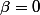
dans les 3 cas, beta va être hors de son domaine de définition !!!
-
camilia89
- Membre Naturel
- Messages: 12
- Enregistré le: 11 Déc 2014, 15:07
-
 par camilia89 » 12 Déc 2014, 12:44
par camilia89 » 12 Déc 2014, 12:44
Ben314 a écrit:La dérivée de
))
est
t^\beta)
Donc, si
=x^\beta-ay^\beta-(1-a)z^\beta\)
alors
=\ln(x)x^\beta-a\ln(y)y^\beta-(1-a)\ln(z)z^\beta)
Donc
>0\ \Leftrightarrow\ h(\beta):=-a\ln(y)\big(\frac{y}{x}\big)^\beta-(1-a)\ln(z)\big(\frac{z}{x}\big)^\beta>-\ln(x))
Ce n'est pas une inéquation que l'on peut résoudre "formellement", mais on peut la résoudre numériquement a condition d'avoir une petite idée du comportement de la fonction

ce qui conduit naturellement... à la dériver...
Sauf qu'il va apparaitre du
)
et du
)
dont on ne connait a priori pas les signes d'où... étude de cas fastidieuse....
SAUF si tu connait dans quel ordre sont les réels x,y et z...
Comme donnée, nous avons toujours
z^\beta => g'(\beta)>0)
est toujours vrai. je sais pas si cette info peut nous aider à résoudre le problème
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 12 Déc 2014, 13:10
par Cliffe » 12 Déc 2014, 13:10
camilia89 a écrit:dans les 3 cas, beta va être hors de son domaine de définition !!!
ah bon ?
Fait l'application numérique pour

et
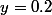
ou encore pour

et

.
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 12 Déc 2014, 13:47
par Cliffe » 12 Déc 2014, 13:47
[CENTER]
 = x^\beta-y^\beta \ \ \ \ \beta \in ]0,1] \ \ \ \ (x,y) \in ]0,1]^2)
[/CENTER]
cas 1 : 
[CENTER]
=0 \Rightarrow \begin{array}{|c|}<br />\hline<br />\underset{x=y}{\underset{\beta \in ]0, 1]}{argmax}} \left ( f_{x-y} \left ( \beta \right ) \right ) = ]0, 1]\\<br />\hline<br />\end{array})
[/CENTER]
cas 2 :  \in ]0,1[^2, \ \ x \ne y)
[CENTER]
 = x^\beta ln (x) - y^\beta ln (y))
[/CENTER]
Soit

tel que
 = 0)
. Par le calcul, on obtient :
[CENTER]
}{ln \left ( x \right )} \right )}{ln \left ( x \right ) - ln \left ( y \right )})
[/CENTER]
_____
cas 2.1 : 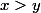
.
[CENTER]Forme de la courbe pour
 \right ) = min \left \{ 1, \beta_0 \right \} \\ \hline \end{array})
[/CENTER]
_____
cas 2.2 : 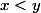
[CENTER]Forme de la courbe pour

:

Forme de la courbe pour

:

On a donc :
 \in ]0,1[, \ \ x < y}{\underset{\beta \in ]0, 1]}{argmax}} \left ( f_{x-y} \left ( \beta \right ) \right ) = 0^+\\ \hline \end{array})
[/CENTER]
cas 3 :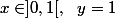
[CENTER]
=x^\beta-1 \Rightarrow \begin{array}{|c|} \hline \underset{x \in ]0,1[, \ \ y = 1}{\underset{\beta \in ]0, 1]}{argmax}} \left ( f_{x-y} \left ( \beta \right ) \right ) = 0^+\\ \hline \end{array})
[/CENTER]
cas 4 :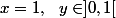
[CENTER]
=1-y^\beta \Rightarrow \begin{array}{|c|} \hline \underset{x = 1, \ \ y \in ]0,1[}{\underset{\beta \in ]0, 1]}{argmax}} \left ( f_{x-y} \left ( \beta \right ) \right ) = 1\\ \hline \end{array})
[/CENTER]
cas 5 :  = (0,1))
[CENTER]
=-1 \Rightarrow \begin{array}{|c|} \hline \underset{(x,y) = (0,1)}{\underset{\beta \in ]0, 1]}{argmax}} \left ( f_{x-y} \left ( \beta \right ) \right ) = ]0,1]\\ \hline \end{array})
[/CENTER]
cas 6 :  = (1,0))
[CENTER]
=1\Rightarrow \begin{array}{|c|} \hline \underset{(x,y) = (1,0)}{\underset{\beta \in ]0, 1]}{argmax}} \left ( f_{x-y} \left ( \beta \right ) \right ) = ]0,1]\\ \hline \end{array})
[/CENTER]
cas 7 : 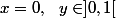
[CENTER]
=-y^\beta\Rightarrow \begin{array}{|c|} \hline \underset{x = 0, \ \ y \in ]0,1[}{\underset{\beta \in ]0, 1]}{argmax}} \left ( f_{x-y} \left ( \beta \right ) \right ) = 1\\ \hline \end{array})
[/CENTER]
cas 8 : 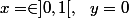
[CENTER]
=x^\beta\Rightarrow \begin{array}{|c|} \hline \underset{x \in ]0,1[, \ \ y = 0}{\underset{\beta \in ]0, 1]}{argmax}} \left ( f_{x-y} \left ( \beta \right ) \right ) = 0^+\\ \hline \end{array})
[/CENTER]
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités


[/CENTER]
.
est
alors
ce qui conduit naturellement... à la dériver...
et du
dont on ne connait a priori pas les signes d'où... étude de cas fastidieuse....
est
alors
ce qui conduit naturellement... à la dériver...
et du
dont on ne connait a priori pas les signes d'où... étude de cas fastidieuse....

