[Résolu] Equation fonctionnelle [TS]
36 messages
- Page 2 sur 2 - 1, 2
par paquito » 30 Sep 2014, 14:12
Je reviens sur mon post précédent ou j'étais arrivé à =f'(x))
; on a donc:
dt=\bigint_{0}^{x}f'(t+1)dt)
, soit =f(x)+f(1))
et puisque =1)
, on obtient pour tout n,=f(n)+1)
donc f(n) est la suite arithmétique de premier terme 
et de raison 
. Je crois qu'il faudrait essayer de prouver qu'il n'y a pas d'autres solution que l'application identique.
par mathelot » 30 Sep 2014, 14:19
Propriété 3 les entiers N avec facteur premier p=4k+3 et valuation p-adique impaire
ne sont pas somme de deux carrés. impossible.
donc déja, je sais pas comment on peut calculer f(N) dans ce cas.
sinon,
théorème tout entier N est somme de quatre carrés
Définition (mathelot) : on dit que n est "cédant" si)
est calculable.
;
(r^2+t^2)=(nr-mt)^2+(mr+nt)^2)
(r^2+t^2)=(n(r-t)-m(t+r))^2+(n(r+t)-m(t-r))^2)
sont ils cédants par récurrence (forte) ?
et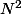 
sont chacun la somme de deux entiers "cédants", et après, j'étais coincé, car les "cédants" ne sont nécessairement stables par additions .
ne sont pas somme de deux carrés. impossible.
donc déja, je sais pas comment on peut calculer f(N) dans ce cas.
sinon,
théorème tout entier N est somme de quatre carrés
Définition (mathelot) : on dit que n est "cédant" si
sont ils cédants par récurrence (forte) ?
par Ben314 » 30 Sep 2014, 16:03
En fait, si on note C l'ensemble des entiers "cédants" on a :
(0) 0 et 1 sont dans C.
(1) Si m et n sont dans C alors n²+m² est aussi dans C.
mais on a aussi
(2) Si m et n²+m² sont dans C alors n est aussi dans C.
A mon sens, la question est alors de savoir si ces trois hypothèses impliquent que C=N ou pas...
(0) 0 et 1 sont dans C.
(1) Si m et n sont dans C alors n²+m² est aussi dans C.
mais on a aussi
(2) Si m et n²+m² sont dans C alors n est aussi dans C.
A mon sens, la question est alors de savoir si ces trois hypothèses impliquent que C=N ou pas...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par paquito » 30 Sep 2014, 17:23
Si n est distinct de=f(m^2)+f(n^2)\neq f(2m^2))
car sinon on aurait f(2m^2)-f(m^2)=f(n^2), ce qui entraînerait f(2m^2)=f(m^2)+f(n^2), d'où f(m^2)=f(n^2) et f prendrait une infinité de fois la même valeur f(m^2+1)=f(n^2+1) puis par récurrence f(m^2+k)=f(n^2+k), donc la suite f(n) serait constante à partir d'un certain rang, ce qui est possible, si l'on pose f(n)=n pour n\leq 18et f(n)=o pour n>18. Ce qui fournit une autre solution.
Si on exclus ces 2 solutions, il existe un entier n tel que f(n)>n; cet ensemble non-vide posséde un plus petit élément n_0, et après je n'ai pas cherché.
Si on exclus ces 2 solutions, il existe un entier n tel que f(n)>n; cet ensemble non-vide posséde un plus petit élément n_0, et après je n'ai pas cherché.
par zygomatique » 30 Sep 2014, 19:34
pour compléter les relations trouvées précédemment :::
pour tous entiers p, q on a aussi
^2 + (qn)^2) = f((pm)^2) + f((qn)^2) =f^2(pm) + f^2(qn))
en particulier
pour n = 0^2) = f^2(pm))
pour n = mm^2)= f^2(pm) + f^2(qm))
d'autre part on a aussi plus directement^2) = f^2(m^k))
sans oublier que :::
si n = m alors = 2f(m)^2)
on en déduit que l'image d'un pair (impair) est pair (impair) puisqu'un entier et son carré ont même parité ....
 = f(m)^2 + 1 = f(m^2) + 1)
donc = 2f^2(2^km))
.... mais j'arrive toujours pas à gratter le bon truc ... de tête ....
:hum:
pour tous entiers p, q on a aussi
en particulier
pour n = 0
pour n = m
d'autre part on a aussi plus directement
sans oublier que :::
si n = m alors
on en déduit que l'image d'un pair (impair) est pair (impair) puisqu'un entier et son carré ont même parité ....
donc
.... mais j'arrive toujours pas à gratter le bon truc ... de tête ....
:hum:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
par paquito » 01 Oct 2014, 11:16
Dans un premier temps essayons d'exclure le cas )
vérifiant >n)
( (n_1+1)^2)
, d'où 
et >f(2n_1^2)>f^2(n_1)+f^2(n_1)=n_1^2+n_1^2)
. il y a contradiction et donc f est l'identité.
En fait c'est l'injectivité qui est difficile (d'ailleurs je n'ai eu le courage de montrer que=0 n=0)
. Ce qui m'étonnes, c'est que cet exercice soit donné en TS???
En fait c'est l'injectivité qui est difficile (d'ailleurs je n'ai eu le courage de montrer que
par Ben314 » 01 Oct 2014, 14:10
J'ai peut-être une solution :
Lemme : Pour tout entier
, il existe des entiers naturels 
tous les 3 strictement plus petits que 
tels que 
.
Preuve : L'intervalle
est de longueur 
donc contient au moins un entier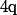 
et on vérifie aisément que
; 
; 
est solution du problème.
On montre alors en utilisant une récurrence forte que=n)
pour tout entier naturel :
Amorce : Pour
voir le post. du 29/09/2014 de Mikihisa.
Hérédité : Soit. On suppose que, pour tout entier naturel 
on a =k)
(récurrence forte).
Le lemme nous dit qu'il existe
(et donc =a\ ,\ f(b)=b\ ,\ f(c)=c\)
) tels que 
.
On a^2+a^2=f(n)^2+f(a)^2=f(n^2+a^2)=f(b^2+c^2)=f(b)^2+f(c)^2=b^2+c^2\)
d'où^2=b^2+c^2-a^2=n^2\)
et donc =n\)
Lemme : Pour tout entier
Preuve : L'intervalle
On montre alors en utilisant une récurrence forte que
Amorce : Pour
Hérédité : Soit
Le lemme nous dit qu'il existe
On a
d'où
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par paquito » 01 Oct 2014, 16:16
mathelot a écrit:pourquoi ?
c'est parce que j'ai fait une faute de frappe!
par paquito » 01 Oct 2014, 16:33
Je me demande toujours comment trouver une piste avec certains exos du concours général! ici, j'ai cherché vainement a prouver que f était strictement croissante; peine perdu, il fallait utiliser des identités remarquables qui arrivent comme un cheveux sur la soupe; c'est joli, mais comment avoir l'idée? il y a d'autres exos du concours général plus abordables!
par chan79 » 01 Oct 2014, 16:40
paquito a écrit:Je me demande toujours comment trouver une piste avec certains exos du concours général! ici, j'ai cherché vainement a prouver que f était strictement croissante; peine perdu, il fallait utiliser des identités remarquables qui arrivent comme un cheveux sur la soupe; c'est joli, mais comment avoir l'idée? il y a d'autres exos du concours général plus abordables!
Voir le lien ci dessus pour une correction détaillée
par zygomatique » 01 Oct 2014, 17:06
chan79 a écrit:Voir le lien ci dessus pour une correction detaillee
merci pour le lien .... et je suis content d'avoir "commencer" comme cette preuve .... :ptdr:
après je voulais aussi essayer de prouver une (stricte) croissance ...
par contre j'avais bien penser à une récurrence forte .... mais sans une étude fine pour progresser de pair en pair ou d'impair en impair et arriver à ces deux égalités remarquables .... :mur:
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
36 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :