Effectivement, c'est un exercice un peu spécial; déjà, il faut modifier le résultat à démontrer qui devient :pour tout
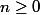
,
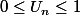
car l'énoncé n'est pas cohérent.
l'initialisation est une donnée de l'énoncé.
l'hypothèse de récurrence va être : pour un entier
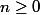
,
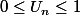
commençons par établir
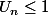
, comme te l'a montré ericovitchi,
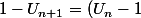^2)
donc
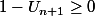
et
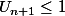
;
ce qui est déroutant dans cette partie de la démonstration, c'est que l'hypothèse de récurrence ne sert strictement à rien! Passons à la deuxième étape.
On a
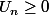
( hypothèse de récurrence) et on sait que
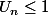
( hypothèse de récurrence) , donc
 \leq 2)
d'où
\geq 0)
et donc :
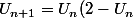 \geq 0)
, ce qui achève la démonstration. (la conclusion est toujours la même)
Ce qu' a voulu te montrer ericovitchi, c'est comment construire les premiers termes de la suite à l'aide de la fonction
=x(2-x))
et de la droite d'équation
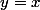
, pour constater qu'elle était croissante et qu les termes se rapprochaient de

.
Ne t'inquiète pas si cet exercice t'a perturbé; il est vraiment très spécial et en plus ne fait pas vraiment travailler la récurrence.

 [/URL]
[/URL]