Limite au voisinage de l'infini
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mimod
- Messages: 2
- Enregistré le: 08 Sep 2013, 14:34
-
 par mimod » 31 Juil 2014, 01:15
par mimod » 31 Juil 2014, 01:15
Bonsoir,
X est une variable aléatoire à densité, de fonction de répartition

et E(X) existe.
Je dois montrer que
=0)
.
Merci d'avance de bien vouloir m'aider.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 31 Juil 2014, 11:47
par zygomatique » 31 Juil 2014, 11:47
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Emolga
- Membre Naturel
- Messages: 10
- Enregistré le: 29 Juil 2014, 15:19
-
 par Emolga » 31 Juil 2014, 16:55
par Emolga » 31 Juil 2014, 16:55
mimod a écrit:X est une variable aléatoire à densité, de fonction de répartition

et E(X) existe.
Je dois montrer que
=0)
.
La fonction de répartition de la variable aléatoire

sur

est:
 = P(X \in ]-\infty, x])= P(X \leq x))
.
Propriétés: la fonction
)
est croissante continue à droite et
= 0; \lim_{ x\to +\infty} F_X (x)= 1)

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 31 Juil 2014, 18:02
par zygomatique » 31 Juil 2014, 18:02
Emolga a écrit:La fonction de répartition de la variable aléatoire

sur

est:
 = P(X \in ]-\infty, x])= P(X \leq x))
.
Propriétés: la fonction
)
est croissante continue à droite et
= 0; \lim_{ x\to +\infty} F_X (x)= 1)
ça ne suffit pas cer on a des limites du type
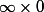
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 31 Juil 2014, 20:19
par jlb » 31 Juil 2014, 20:19
intégration par partie à partir de l'espérance?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités