Petite question "élémentaire"
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mr_pyer
- Membre Relatif
- Messages: 137
- Enregistré le: 07 Avr 2013, 20:42
-
 par mr_pyer » 23 Mai 2014, 15:30
par mr_pyer » 23 Mai 2014, 15:30
Bonjour à tous !

et

sont deux nombres positifs. La fonction

est croissante sur
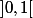
ssi

.
Quelqu'un peut-il m'aider à le démontrer ?
Merci d'avance...
P.S. : J'ai une solution qui est loin d'être satisfaisante. En fait je suis sûr que je loupe un argument de convexité caché quelque part...
-
mr_pyer
- Membre Relatif
- Messages: 137
- Enregistré le: 07 Avr 2013, 20:42
-
 par mr_pyer » 23 Mai 2014, 15:41
par mr_pyer » 23 Mai 2014, 15:41
Je me réponds tout seul :id:
Il suffit d'écrire
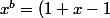^b = \sum_{k\ge0} C_b^k (x-1)^k)
...
Edit. Enfin, ça résout le problème lorsque a=0 :mur:.
-
Robic
- Membre Irrationnel
- Messages: 1084
- Enregistré le: 03 Mai 2013, 11:00
-
 par Robic » 23 Mai 2014, 22:35
par Robic » 23 Mai 2014, 22:35
Une petite idée : le produit de deux fonctions croissantes n'est pas forcément une fonction croissante. Mais si elles sont positives, c'est vrai. Ici, les facteurs
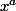
,

et
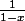
correspondent à des fonctions positives, puisqu'on est sur ]0,1[. De plus la troisième fonction est croissante. Donc le problème revient à étudier la fonction
)
. Peut-être n'est-il pas trop compliqué de la dériver ?
Je viens de commencer les calculs... mais je ne trouve pas le bon résultat (et puis il y a pas mal de cas particuliers).
-
mr_pyer
- Membre Relatif
- Messages: 137
- Enregistré le: 07 Avr 2013, 20:42
-
 par mr_pyer » 23 Mai 2014, 23:03
par mr_pyer » 23 Mai 2014, 23:03
Je te remercie de t'intéresser à mon problème :we:
Ce que tu me proposes ne fonctionne pas avec a=b=1 puisque
)
n'est pas croissante sur ]0,1[ alors que

l'est.
Je sais démontrer la caractérisation
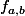
croissante sur ]0,1[ ssi

à l'aide de propriétés des fonctions hypergéométriques mais je suis convaincu qu'il y a plus simple : même un élève de 1ère comprendrait la question... !
-
Robic
- Membre Irrationnel
- Messages: 1084
- Enregistré le: 03 Mai 2013, 11:00
-
 par Robic » 24 Mai 2014, 02:33
par Robic » 24 Mai 2014, 02:33
Ah oui, en fait mon idée ne donnerait qu'une condition suffisante : si
)
était croissante, alors la fonction complète le serait. Mais ce n'est pas réciproque.

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 24 Mai 2014, 08:26
par fatal_error » 24 Mai 2014, 08:26
slt,
un peu brouillon mais ca doit se tenir
=x^a (\frac{ 1-x^b}{1-x}))
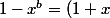(1-x^{b-1}))
donc
 = \frac{1+x}{1-x} x^a(1-x^{b-1}))
le produit de deux fonctions croissantes est une fion croissante.
EDIT: seulement si elles sont positives (j'ai pas regardé la positivité....)
(1+x)/(1-x) a pour dérivée 2/(1-x^2)..
donc on veut trouver a et b tels que
)
est croissant.
On factorise par l'angle moitié:
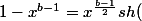)
sh est croissante sur R
on cherche donc la croissance de :

puis pour x positif, le signe est donné par le signe de

la vie est une fête

-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 24 Mai 2014, 09:20
par jlb » 24 Mai 2014, 09:20
Salut, petit pb, non?
fatal_error a écrit:slt,
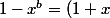(1-x^{b-1}))
donc....[/TEX]

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 24 Mai 2014, 09:57
par fatal_error » 24 Mai 2014, 09:57
roh p******, superbe factorisation!
la vie est une fête

-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 24 Mai 2014, 10:45
par jlb » 24 Mai 2014, 10:45
bon, sauf grosses erreurs fortement envisageable!!, on dérive f, il reste à étudier le signe de h(x)= a + (1-a)x-(a+b)x^b + (a+b-1)x^(b+1)
h'(x) = (1-a) - b(a+b)x^(b-1) + (b+1)(a+b-1)x^b
h''(x)= -b(b-1)(a+b)x^(b-2) + b(b+1)(a+b-1)x^(b-1)
avec une petite considération sur l'expression de h'' et h''(1) = b(2a+b-1)=>0, on en déduit que h''(x)=>0 sur ]0,1[
ainsi h' est croissante sur ]0,1[ mais h'(1)=0 donc h'(x)<=0 sur ]0,1[
et donc h est décroissante sur ]0,1[ mais h(1)=0 donc h est positive sur ]0,1[ et donc f est croissante sur ]0,1[ voili, voilou, effectivement niveau lycée...
@ mr_pryer: c'est quoi une fct hyper géométrique? et comment tu obtiens le résultat par curiosité car pour moi cela n'a aucun intérêt tout cela!!! tu cherches ce résultat dans quel but? cela a-t-il une application sympa? merci
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 24 Mai 2014, 11:23
par jlb » 24 Mai 2014, 11:23
salut, a priori, en dérivant f et en étudiant le signe de la dérivée, le résultat et la condition apparaissent .
{En gros, étude sérieuse de h(x) = a + (1-a)x - (a+b)x^b +(a+b-1)x^(b+1), dérivée seconde avec 2 cas à traiter, utilisation de h(1), h'(1),h''(1) qui donne des valeurs intéressantes}
après, il faut vérifier, c'est loin d'être sur!!! elle sert à quoi cette fct f?? c'est quoi une fct hypergéométrique et comment obtiens-tu le résultat?
-
mr_pyer
- Membre Relatif
- Messages: 137
- Enregistré le: 07 Avr 2013, 20:42
-
 par mr_pyer » 24 Mai 2014, 14:14
par mr_pyer » 24 Mai 2014, 14:14
c'est quoi une fct hypergéométrique et comment obtiens-tu le résultat?
Par exemple on note
 = \sum_{n\ge0} \frac{(a)_n(b)_n}{(c)_nn!}z^n)
où
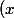_n=x(x+1)\cdots(x+n-1))
désigne le symbole de Pochhammer.
)
est log-concave sous certaines conditions. Ainsi, la fonction

est log-concave lorsque b1. De là on déduit la propriété assez facilement.
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 25 Mai 2014, 10:50
par jlb » 25 Mai 2014, 10:50
Ok, merci et on utilise cela dans quel domaine?
-
mr_pyer
- Membre Relatif
- Messages: 137
- Enregistré le: 07 Avr 2013, 20:42
-
 par mr_pyer » 25 Mai 2014, 12:09
par mr_pyer » 25 Mai 2014, 12:09
Ici cela permet de démontrer que
)
a une loi auto-décomposable, où
}{\Gamma(a)\Gamma(b)}x^{a-1}(1-x)^{b-1}dx,\quad x\in]0,1[)
suit la loi Beta de paramètre (a,b).
Sinon ces fonctions hyper-géométriques apparaissent comme solutions de certaines équations différentielles. Un exemple,

est solution de l'équation différentielle
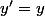
, on peut aussi écrire
)
.
C'est pas l'exemple le plus impressionnant je le conçois...
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 26 Mai 2014, 15:32
par wserdx » 26 Mai 2014, 15:32
Bonjour,
J'ai jeté un oeil à ce problème qui me semble assez difficile!
La dérivée logarithmique vaut :

J'ai cherché les limites en 0 et 1 de ce machin qui sont respectivement

et
)
. (note pour la deuxième limite, j'ai demandé à wolfram... :hein: )
Une condition nécessaire pour que la fonction de départ soit croissante est donc :

Pour la condition suffisante, je ne vois pas trop :hum: (étudier la décroissance de la dérivée ?)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 93 invités