Valeurs propres

par **mehdi-128** » 16 Mai 2007, 18:57

Sout u un endomorphisme antisymétrique,soit lambda valeur propre complexe ou lambda non nulle.Montrer que lambda est imaginaire pur.

par **yos** » 16 Mai 2007, 19:25

Ah c'est déjà plus rigolo.
Bon j'ai travaillé matriciellement : A matrice de u dans une bo :

et X vecteur propre (dans

) pour la vp complexe

.
On a

, donc

.

par **mehdi-128** » 16 Mai 2007, 19:37

lol merci,désolé de te donner des trucs trop faciles....
Juste une question de notation pourquoi y a pas de barre sur transposée de X ?

par **mehdi-128** » 16 Mai 2007, 20:00

En fait j'ai pas compris l'histoire des conjugués....

par **cesar** » 16 Mai 2007, 20:17

yos a écrit:Ah c'est déjà plus rigolo.
Bon j'ai travaillé matriciellement : A matrice de u dans une bo : et X vecteur propre (dans ) pour la vp complexe .
On a , donc .

et en dimension infinie, on fait comment ???

par **mehdi-128** » 16 Mai 2007, 20:21

tu pourrait pas m'expliquer le raisonnement stp ?Je vois pas c'est ou qu'on met des conjugués en fait...

par **yos** » 16 Mai 2007, 20:28

L'égalité

vient du fait que la transposée d'une matrice (1,1) c'est elle-même.
Le premier membre se calcule ainsi

.
Le second membre de même.
Tenir compte du fait que A est réelle (donc

est valeur propre de A pour le vecteur propre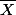

.
Est-ce que ça répond à ta question?

Pour la question de Cesar, je dois dire que si j'ai travaillé matriciellement, c'est parce que j'ai des scrupules à appliquer l'endomorphisme réel u à des vecteurs de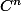

. Mais ce sont sans doutes des précautions d'amateur. Du coup en dimension infinie,... faut voir.

par **mehdi-128** » 16 Mai 2007, 20:40

en fait j'ai compris le raisonnement mon probleme c'est avec les conjugués,je vois pas c'est quand qu'on doit mettre un conjugué....

par **yos** » 16 Mai 2007, 20:48

C'est moi qui comprend pas ta question : je mets des conjugués pour faire intervenir

, le but étant d'arriver à

, ce qui caractérise un imaginaire pur.

par **mehdi-128** » 16 Mai 2007, 21:03

Ok le truc que j'avais pas compris c'est que dans un espace complexe la matrice associée a u(x) ou A est la matrice de u c'est:

Y=A*X(barre) je viens de le démontrer.

par **yos** » 16 Mai 2007, 21:13

mehdi-128 a écrit:Ok le truc que j'avais pas compris c'est que dans un espace complexe la matrice associée a u(x) ou A est la matrice de u c'est:

Y=A*X(barre) je viens de le démontrer.

Je te suis pas.
Si x est un vecteur de E (que l'on identifie à

), alors u(x) ou AX c'est pareil (identification classique via une base de E).
Sinon, on peut pas parler de u(x) à moins de faire une extension du corps des scalaires :

et je suis pas sûr que ça te plaise.
D'où le calcul matriciel qui lui s'étend naturellement au domaine complexe.

par **jahbromo** » 17 Mai 2007, 11:31

mehdi-128 a écrit:Sout u un endomorphisme antisymétrique,soit lambda valeur propre complexe ou lambda non nulle.Montrer que lambda est imaginaire pur.

mon ami cest evident.la definition du valeur propre et l'hypotheses "ansymetrie montre Re(l)=-Re(l) dont Re(l) =0 ou l est valeuer propres de u

par **yos** » 17 Mai 2007, 12:00

jahbromo a écrit:mon ami cest evident.la definition du valeur propre et l'hypotheses "ansymetrie montre Re(l)=-Re(l) dont Re(l) =0 ou l est valeuer propres de u

Tu peux détailler s'il te plait?

Valeurs propres

valeurs propres

Qui est en ligne