Une limite très difficile
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 13 Jan 2015, 22:04
par adamNIDO » 13 Jan 2015, 22:04
votre aide sil vous plait
-
mathelot
 par mathelot » 14 Jan 2015, 09:33
par mathelot » 14 Jan 2015, 09:33
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 14 Jan 2015, 10:01
par adamNIDO » 14 Jan 2015, 10:01
mathelot a écrit:=1,\qquad u(n+\frac{1}{2})>\sqrt{n})
mais concernant
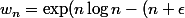\log(n+\epsilon))\quad n\in \mathbb{N}^*;\quad \epsilon \in ]0,1[)
@paquito tromper de l'expression de
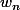
et il a montrer qu'il diverge vers

mais
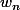
converge vers

quand
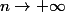
donc on peut dire que f n'admet pas de limite mais on peux pas dire qu'il diverge vers

comme il a fait @paquito
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 14 Jan 2015, 10:36
par paquito » 14 Jan 2015, 10:36
Il suffit de programmer le graphe de f(x)=\frac{x^x}{E(x)^E(x)} sur une calculatrice avec 1Sinon, normalement, ln(a/b)=ln(a)-ln(b).
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 14 Jan 2015, 10:44
par adamNIDO » 14 Jan 2015, 10:44
paquito a écrit:Il suffit de programmer le graphe de
=\frac{x^x}{E(x)^E(x)})
sur une calculatrice avec 1<x<20 et 0<y<50 pour voir ce qui se passe.
Sinon, normalement, ln(a/b)=ln(a)-ln(b).
comme avez dit que " normalement, ln(a/b)=ln(a)-ln(b)"
donc
=n\log n-(n+\epsilon)\log(n+\epsilon))
et pas
=(n+\epsilon)ln(n+\epsilon)-nln)
ce qui veut dire que
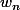
converge vers

quand
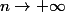
donc on peut dire que f n'admet pas de limite mais on peux pas dire qu'il diverge vers

comme avez fait
n'est pas
-
BiancoAngelo
- Membre Rationnel
- Messages: 585
- Enregistré le: 12 Déc 2011, 23:06
-
 par BiancoAngelo » 14 Jan 2015, 11:46
par BiancoAngelo » 14 Jan 2015, 11:46
Hello !
Si ça peut aider...

-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 14 Jan 2015, 11:57
par adamNIDO » 14 Jan 2015, 11:57
BiancoAngelo a écrit:Hello !
Si ça peut aider...

merci mais pourquoi
personne ne repond directement a ma question? alors
@paquito a ete tromper dans l'expression de
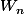
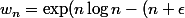\log(n+\epsilon))\quad n\in \mathbb{N}^*;\quad \epsilon \in ]0,1[) n'est ce pas ??
n'est ce pas ??mais
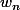
converge vers

quand
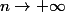
donc
on peut dire que f n'admet pas de limite mais on peux pas dire qu'il diverge vers  comme il a fait
comme il a fait @paquito
-
assojako
- Membre Naturel
- Messages: 20
- Enregistré le: 16 Oct 2014, 14:10
-
 par assojako » 14 Jan 2015, 15:59
par assojako » 14 Jan 2015, 15:59
on a lim_{x;);)}(1+(a/x))^{x}=e^{a}
et x=[x]+a tq 0
donc la limite chercher est si x;)R/{N}:
= lim_{x;);)}(1+(a/([x])))^{[x]}[[x]+a]=e^{a};)=;)
Mais si x;)N limite chercher est 1
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 14 Jan 2015, 16:21
par arnaud32 » 14 Jan 2015, 16:21
la reponse c'est que f n'a pas de limite en +oo
et pour le justifier tu trouves deux suites de reels qui tendent vers +oo et dont les images par f ont des limites differentes
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
sur une calculatrice avec 1<x<20 et 0<y<50 pour voir ce qui se passe.

