Bonjour
Voici mon problème :
On a un sac remplit de 500 000 000 billes, tous de couleur bleu à l'exception de 320 000 qui sont vertes. En un an on en prend 27000 de manière aléatoire, une par une pour les peindre en rouge et en les remettants à chaque fois. Quelle est la probabilité après un an d'avoir peint une même bille verte 2 fois en rouge ?
C'est plus le chemin de calcul que le résultat qui m'intéresse.
Merci
Une énigme de proba avec des billes
3 messages
- Page 1 sur 1
Re: Une énigme de proba avec des billes
Parce que quand tu tires une bille rouge, tu la peins une seconde fois en rouge ???
Re: Une énigme de proba avec des billes
Salut,
Ca me semble plus que coton d'avoir la valeur exacte (et pas évident du tout d'avoir une valeur approximative).
Pour calculer la proba qu'au bout de
qu'au bout de  tirage on n'ait jamais repeint une deuxième fois une verte (à l'origine) en rouge, on peut dire que c'est la somme pour
tirage on n'ait jamais repeint une deuxième fois une verte (à l'origine) en rouge, on peut dire que c'est la somme pour 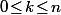 de la proba d'avoir tiré
de la proba d'avoir tiré  vertes différentes et
vertes différentes et 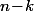 bleues quelconques .
bleues quelconques .
Le nombre de suites BVVBVBV.... contenant V et
V et 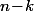 B est
B est 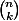 (coeff binomial) et, pour une telle suite donnée, la proba que ça corresponde au tirage effectué (avec des vertes différentes) est
(coeff binomial) et, pour une telle suite donnée, la proba que ça corresponde au tirage effectué (avec des vertes différentes) est }{t}\Big(\dfrac{b}{t}\Big)^{n-k}=k!{v\choose k}\dfrac{b^{n-k}}{t^n}) si
si 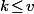 et 0 sinon.
et 0 sinon.
(où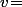 Nb de vertes au départ ;
Nb de vertes au départ ; 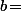 Nb de bleue au départ ;
Nb de bleue au départ ; 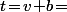 Nb total de billes)
Nb total de billes)
Donc^{\! n}\,\sum_{k=0}^{\text{min}(n,v\!)}\!\!\!\!k!{n \choose k}{v\choose k}b^{-k})
Mais je ne sais pas calculer explicitement ce type de sommes et je ne crois pas (pas sûr...) que ce soit exprimable avec les fonctions "élémentaires" du dénombrement, mais il y a sans doute des fonctions "spéciales" dédiées.
Après, on peut éventuellement (à voir...) faire une estimation de la somme en question, mais tant qu'à faire des estimations, je pense que le plus simple serait plutôt de regarder bille par bille la loi qui donne le nombre de fois qu'elle a été tirée : cette loi est on ne peut plus simple et c'est la même pour chaque bille mais le problème, c'est qu'elles ne sont pas indépendantes et il faut sans doute estimer cette "non indépendance" pour voir quelle erreur on commet en faisant le calcul comme si les lois étaient indépendantes (ou alors ne tenir compte que de la dépendance 2 à 2 des lois ou une idée du même style...).
Ca me semble plus que coton d'avoir la valeur exacte (et pas évident du tout d'avoir une valeur approximative).
Pour calculer la proba
Le nombre de suites BVVBVBV.... contenant
(où
Donc
Mais je ne sais pas calculer explicitement ce type de sommes et je ne crois pas (pas sûr...) que ce soit exprimable avec les fonctions "élémentaires" du dénombrement, mais il y a sans doute des fonctions "spéciales" dédiées.
Après, on peut éventuellement (à voir...) faire une estimation de la somme en question, mais tant qu'à faire des estimations, je pense que le plus simple serait plutôt de regarder bille par bille la loi qui donne le nombre de fois qu'elle a été tirée : cette loi est on ne peut plus simple et c'est la même pour chaque bille mais le problème, c'est qu'elles ne sont pas indépendantes et il faut sans doute estimer cette "non indépendance" pour voir quelle erreur on commet en faisant le calcul comme si les lois étaient indépendantes (ou alors ne tenir compte que de la dépendance 2 à 2 des lois ou une idée du même style...).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
