Trouver un contre exemple
15 messages
- Page 1 sur 1
Trouver un contre exemple
Bonjour,
Je souhaite trouver un contre exemple de la proposition suivante :
Soit f appartient à la classe C^1 => f appartient à la classe C^2
Je souhaite trouver un contre exemple de la proposition suivante :
Soit f appartient à la classe C^1 => f appartient à la classe C^2
Re: Trouver un contre exemple
Bonjour,
Une primitive de la fonction est un contre exemple. Une telle primitive existe puisque f est continue. De plus,
est un contre exemple. Une telle primitive existe puisque f est continue. De plus,  est
est 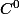 mais pas
mais pas  . Par conséquent, ses primitives sont
. Par conséquent, ses primitives sont  mais pas
mais pas  .
.
Une primitive de la fonction
Re: Trouver un contre exemple
Mais ici on ne chercher pas une primitive mais une dérivée. Du coup, j'ai du mal à comprendre. Pouvez-vous détaillez s'il vous plaît ?
Re: Trouver un contre exemple
Ou un autre exemple avec une formule directe : la fonction définie par
=x^3\sin\frac{1}{x}) prolongée par continuité en 0 par
prolongée par continuité en 0 par =0)
Sa dérivée est pour tout x non nul :=3x^2\sin(\frac{1}{x})-x\cos\frac{1}{x}) , qui a pour limite 0 en zéro, et on calcule explicitement f'(0) en utilisant la définition du nombre dérivé
, qui a pour limite 0 en zéro, et on calcule explicitement f'(0) en utilisant la définition du nombre dérivé
-f(0)}{h}\Big)=\lim_{h\rightarrow 0}\Big(h^2 \sin\frac{1}{h}\Big)=0)
La dérivée est bien continue en 0 donc f est de classe C1.
Mais elle n'est pas dérivable en 0.
Ou encore la fonction=x^4\sin\frac{1}{x}) qui est deux fois dérivable, mais la dérivée seconde n'est pas continue en zéro.
qui est deux fois dérivable, mais la dérivée seconde n'est pas continue en zéro.
Sa dérivée est pour tout x non nul :
La dérivée est bien continue en 0 donc f est de classe C1.
Mais elle n'est pas dérivable en 0.
Ou encore la fonction
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Trouver un contre exemple
dellamab a écrit:Mais ici on ne chercher pas une primitive mais une dérivée. Du coup, j'ai du mal à comprendre. Pouvez-vous détaillez s'il vous plaît ?
Relisez bien ce que vous a écrit Rhaegar : soit f une primitive de |x|. Alors f est dérivable (sa dérivée est |x|) est sa dérivée est continue, donc f est de classe C1. Mais la valeur absolue n'est pas dérivable en 0, donc f n'admet pas de dérivée seconde en 0.
Donc f est un exemple de fonction de classe C1 et qui n'est pas de classe C2.
On peut définir f par partie :
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Trouver un contre exemple
Considére la fonction  . Cette fonction est dérivable et sa dérivée est
. Cette fonction est dérivable et sa dérivée est  .
. 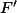 est continue. On en déduit que
est continue. On en déduit que  est une fonction de classe
est une fonction de classe  puisque c'est une fonction dérivable dont la dérivée
puisque c'est une fonction dérivable dont la dérivée 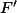 est continue.
est continue.
Si on s'intéresse maintenant à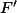 , on remarque qu'elle n'est pas dérivable en 0 (et donc pas dérivable sur
, on remarque qu'elle n'est pas dérivable en 0 (et donc pas dérivable sur  ). Elle n'est donc pas de classe
). Elle n'est donc pas de classe  . Par conséquent, on ne peut pas dériver
. Par conséquent, on ne peut pas dériver  deux fois et donc
deux fois et donc  n'est pas de classe
n'est pas de classe  .
.
Si on s'intéresse maintenant à
Re: Trouver un contre exemple
@Rhaegar, ok j'ai bien compris le raisonnement. Par contre je ne comprends pas comment vous trouvez que la dérivé de F(x) est égale à |x|, parce que quand je fais sa dérivée je trouve : (6*x^2*abs(x)-2*x^3)/(2*abs(x))^2
Re: Trouver un contre exemple
(6*x^2*abs(x)-2*x^3)/(2*abs(x))^2 en "lisible", c'est, après simplifications (habituez vous à faire les simplifications...

Mais maintenant il va falloir que vous expliquiez comment vous obtenez cette formule car elle est un peu fausse.
en effet, vous utilisez')
Mais quelle est la dérivée de la fonction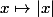 ... ?
... ?
Mais maintenant il va falloir que vous expliquiez comment vous obtenez cette formule car elle est un peu fausse.
en effet, vous utilisez
Mais quelle est la dérivée de la fonction
Modifié en dernier par hdci le 03 Mar 2021, 18:03, modifié 1 fois.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Trouver un contre exemple
Comme l'a justifié hdci, il suffit de séparer les cas x>0 et x<0. Il faut ensuite "recoller les morceaux". En gros, on prolonge notre fonction 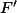 par continuité en 0. On pose une fonction g vérifiant
par continuité en 0. On pose une fonction g vérifiant
On a donc = F'(x) = -x) si x<0,
si x<0,  = 0) et
et  = F'(x) = x) si x > 0. La fonction g est bien continue. On veut maintenant justifier que F' = g. Il faut pour cela vérifier que la dérivée en 0 de
si x > 0. La fonction g est bien continue. On veut maintenant justifier que F' = g. Il faut pour cela vérifier que la dérivée en 0 de  existe et est bien 0. Pour cela il faut revenir à la définition de la dérivée avec les accroissements finis, c'est à dire montrer que
existe et est bien 0. Pour cela il faut revenir à la définition de la dérivée avec les accroissements finis, c'est à dire montrer que -F(0)}{x-0} = 0) , ce qui est bien le cas.
, ce qui est bien le cas.
On a donc
Re: Trouver un contre exemple
Bonjour, pourquoi ne pas prendre directement la fonction =\frac{1}{2} x|x|) définie sur
définie sur  ? Cela simplifie les choses je trouve.
? Cela simplifie les choses je trouve.
Re: Trouver un contre exemple
Oui effectivement, c'est la même fonction puisque  . ça simplifie les choses.
. ça simplifie les choses.
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
