Bonsoir,
Je bloque sur cet exercice :
Soit n un entier non nul et f un l'endomorphisme qui a la matrice M associe la transposée de M.
1) Vérifier que f est un endomorphisme
2) Calculer son rang, sa trace, son déterminant on pourra écrire la matrice de f dans une base adaptée.
Pour la 1) il faut montrer que f est une application linaire de E dans E (mais e ne vois pas comment faire)
Pouvez vous m'aider
Merci
Transposée d'une matrice
6 messages
- Page 1 sur 1
Re: Transposée d'une matrice
Bonjour,
Clairement f est à valeurs dans E. Ensuite on revient à la caractérisation d'une application linéaire :
Montrer que pour toutes matrices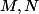 et tout élément
et tout élément  de
de 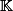 on a :
on a : =\lambda {^tM}+ {^tN})
Ensuite regardes l'effet de cette application sur les matrices de la base canonique de) pour écrire la matrice de l'application "transposée" dans cette base.
pour écrire la matrice de l'application "transposée" dans cette base.
Clairement f est à valeurs dans E. Ensuite on revient à la caractérisation d'une application linéaire :
Montrer que pour toutes matrices
Ensuite regardes l'effet de cette application sur les matrices de la base canonique de
Re: Transposée d'une matrice
Très bien merci
je ne comprend pas très bien " Ensuite regardes l'effet de cette application sur les matrices de la base canonique " sauf dire que la transposée ne change pas les éléments diagonaux..
je ne comprend pas très bien " Ensuite regardes l'effet de cette application sur les matrices de la base canonique " sauf dire que la transposée ne change pas les éléments diagonaux..
Re: Transposée d'une matrice
N'oublies pas qu'il s'agit d'une application linéaire sur l'espace des matrices carrées d'ordre  . Par conséquent quelle est la base canonique de cet espace ? Si
. Par conséquent quelle est la base canonique de cet espace ? Si  est dans la base canonique, que vaut
est dans la base canonique, que vaut ) ?
?
Re: Transposée d'une matrice
Selon ton résultat, l'application "transposée" serait la même que l'application "identité" 
La base canonique de) est la famille des matrices
est la famille des matrices 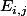 où tous les coefficients sont nuls sauf celui de coordonnées
où tous les coefficients sont nuls sauf celui de coordonnées ) qui vaut
qui vaut  .
.
Par conséquent que vaut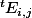 ? Déduis-en la matrice de l'application "transposée" dans la base canonique de
? Déduis-en la matrice de l'application "transposée" dans la base canonique de )

La base canonique de
Par conséquent que vaut
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
