Trace d'une matrice

[zork]

bonjour,

on pose
f:(Mn(R))²-->R
(A,B)--tr(AB)

déterminer noyau de f, rang et signature

pour le noyau:
soit A dans Mn(R)
A dans kerf ssi pour tout B f(A,B)=0 ssi tr(AB)=0 => ssi ssi A=0

pourquoi a-t-on une implication: => ?

pourquoi donne ?


pour la signature:
on considère les matrices symétrique et antysymétriques:
pourquoi Tr(S²)= ?

merci

[ev85]

A dans kerf ssi pour tout B f(A,B)=0 ssi tr(AB)=0 => ssi ssi A=0

pourquoi a-t-on une implication: => ?

Si c'est vrai pour toute matrice B, c'est vrai pour

pourquoi donne ?

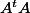
Il faudra que tu fasses le calcul de au moins une fois dans ta vie.

pour la signature:
on considère les matrices symétrique et antysymétriques:
pourquoi Tr(S²)= ?

merci

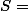
Dire que S est symétrique c'est dire que , ensuite, c'est le calcul de ta vie...