Trace d'une matrice

[barbu23]

Bonsoir,

J'ai un autre problème qui me fait un peu mal dans la tête, le voiçi :

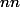
On designe par l'espace des matrices réelles muni de la norme :

Quelle est , pour cette norme, la norme de la forme linéaire :

J'ai essayé de majorer : par , ce n'est pas toujours possible.
Y'a-t-il une autre methode à suivre ?

Merci pour votre aide.

[Nightmare]

Salut,

utilise Cauchy-Schwartz, tu devrais trouver que la norme est égal à la racine carrée de n.

[girdav]

Bonjour,
le fait que la norme d'un application linéaire soit définie comme étant . On sait que ce sup est atteint pour cause de dimension finie.
Vois-tu quel genre de matrice est susceptible d'atteindre ce ?

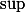
[barbu23]

non, pas du tout :mur:

[barbu23]

Salut,

utilise Cauchy-Schwartz, tu devrais trouver que la norme est égal à la racine carrée de n.

tu veux dire inegalité de cauchy schwartz? :help: :hein:

[girdav]

non, pas du tout :mur:

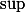
En fait on peut regarder le de pour une matrice de norme .
Il faut rendre aussi grand que possible mais doit rester de norme 1. Pourquoi pas tenter une matrice diagonale?

[barbu23]

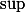
En fait on peut regarder le de pour une matrice de norme .
Il faut rendre aussi grand que possible mais doit rester de norme 1. Pourquoi pas tenter une matrice diagonale?

Oui, parceque là on a la trace de $A $ , donc ce qui nous interesse sont les elements de la diagonale.
mais, si on prend une matrice de norme $ 1 $, à quoi est egale , ça peut être n'importe quoi. nous on cherche une valeur precise je pense non ??? :mur: :marteau: :hein:
Merci pour votre aide

[girdav]

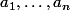
Si on prend une matrice dont les éléments diagonaux sont , alors on doit avoir . Comment majorer ?

[barbu23]

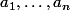
Si on prend une matrice dont les éléments diagonaux sont , alors on doit avoir . Comment majorer ?

si , alors : les

correct ??? et donc :hein: :hein: :hein:

[girdav]

L'inégalité est vraie mais ce n'est sûrement pas la meilleure borne.
Tu peux faire ce qu'indique Nightmare : utiliser Cauchy-Schwartz.

[barbu23]

L'inégalité est vraie mais ce n'est sûrement pas la meilleure borne.
Tu peux faire ce qu'indique Nightmare : utiliser Cauchy-Schwartz.

Voiçi l'inegalité de cauchy schwartz :
Mais je l'applique à quel objet ? on a pas un prduit scalaire ici ??? :hein: :help:

[girdav]

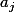
Si, on peut voir la somme comme étant le produit scalaire euclidien du vecteur de composantes par le vecteur contenant que des .

[barbu23]

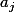
Si, on peut voir la somme comme étant le produit scalaire euclidien du vecteur de composantes par le vecteur contenant que des .

D'accord, alors :

Après, qu'est ce qu'on fait ???? :help: :briques:

[girdav]

On regarde le cas d'égalité?

[barbu23]

On regarde le cas d'égalité?

il y'a egalité quant et sont linéaire, c'est à dire : , c'est à dire : pour
ça veut dire quant , c'est ça ?

[girdav]

Oui, et il reste à trouver le qu'il faut pour que la matrice soit de norme .

[barbu23]

Oui, et il reste à trouver le qu'il faut pour que la matrice soit de norme .

donc ,il suffit de prendre
et donc
Donc : ??? :hein:

[Nightmare]

Ca me va !

[barbu23]

Ca me va !

Ah d'accord, j'ai oublié c'ke t'as dit au debut de la discussion. :zen:
La chose qui me gène ici est qu'on a traité simplement la trace des matrices diagonales. Qu'en est - il pour les autres non diagonales dont la norme est egale à ?
MErci d'avance. :happy3:

[barbu23]

Oui, et il reste à trouver le qu'il faut pour que la matrice soit de norme .

MERCI BEAUCOUP girdav :happy2: