Topologie usuelle sur R^k

par **barbu23** » 29 Mar 2009, 18:23

Bonjour à tous : :happy3:
Je voudrai savoir pourquoi pour la topologie associé à la metrique usuelle de

, les seuls ensembles à la fois ouverts et fermés sont l'ensemle vide et les singletons de

Merci d'avance ! :happy3:

par **leon1789** » 29 Mar 2009, 18:33

les singletons ne sont pas ouverts pour la métrique habituelle :doh:

par **barbu23** » 29 Mar 2009, 18:47

Non qu'est ce que je raconte : :hum:
Les seuls ensembles à la fois ouverts et fermés sont

et

.. désolé pour cet erreur par inadvertance ! :zen: :happy2:

par **leon1789** » 29 Mar 2009, 19:32

Je pense que le point essentiel est de savoir pourquoi les ouverts et fermés de R sont le vide et R lui-même.
Pour R, tu as une démo ?

par **barbu23** » 29 Mar 2009, 19:52

Non ! :hum: :cry: :we:

par **barbu23** » 29 Mar 2009, 19:59

Pour la topologie

usuelle des ouverts de

:

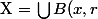Il faut montrer que

n'est pas fermé ! Mais, je ne vois pas comment faire pour la suite ! :hum: :cry:

Merci d'avance de votre aide ! :happy3:

par **ffpower** » 29 Mar 2009, 21:22

Sur R.Si A est un ouvert fermé de R,et si I est un intervalle compact de R:supposons que A inter I diff du vide et diff de I,que dire de t=inf(A inter I)

Topologie usuelle sur R^k

Topologie usuelle sur R^k

Qui est en ligne