Théorème de prolongement
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
par chombier » 06 Juin 2018, 18:53
Bonjour,
J'ai un petit souci avec une preuve du Gourdon, qui a été reprise ici (/!\ c'est le lemme /!\) :
http://math.univ-lyon1.fr/homes-www/gel ... gement.pdfIl s'agit d'un théorème de prolongement. Je comprends très bien la construction de la fonction g, celle de la suite (y_n) (par densité de A dans E (avec epsilon=1/n)), donc je suis d'accord avec ça :
 \leq \frac{1}{n})
Mais je n'arrive vraiment pas à comprendre d'où viens cette inégalité :
, f(y_n)) \leq \frac{1}{n})
Y a-t-il une évidence qui m'échappe ?
Merci d'avance !!
Modifié en dernier par
chombier le 07 Juin 2018, 07:26, modifié 2 fois.
-
Elias
- Habitué(e)
- Messages: 369
- Enregistré le: 07 Fév 2016, 17:20
-
par Elias » 06 Juin 2018, 19:18
Salut,
Ça provient du fait que
 = g (x_n))
(n est un entier non nul fixé)
Par définition, ça veut dire que si tu prends un
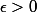
, alors il existe un
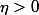
tel que pour tout
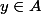
, si
 \leq \eta,)
alors
,f(y)) \leq \epsilon)
Donc ici, on fixe notre entier n non nul et on prend
On a l'existence de notre
.
On sait par densité de A qu'il existe un
dans A tel que
 \leq min(\eta,1/n))
On a alors
 \leq 1/n)
et également
 \leq \eta)
d'où
,f(y_n)) \leq \epsilon = 1/n)
Ps: tu prépares la leçon "prolongement" à l'agrég je suppose ? Bon courage pour la suite.
Pseudo modifié : anciennement Trident2.
-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
par chombier » 06 Juin 2018, 20:15
Merci, je crois que j'ai compris, je reformule pour la forme (ça m'aide !)
D'après l'énoncé,
 = g (x))
Par définition, on peut le reformuler ainsi :
 < \eta_{x, \epsilon} \Rightarrow \delta(f(a), g(x)) < \epsilon)
avec
,
et
:
 < \eta_{x_n, 1/n} \Rightarrow \delta(f(a), g(x_n)) < 1/n)
Et on a notre
!!
Par densité de A, on choisit un
tel que
 < min(1/n, \eta_{x_n, 1/n}))
Ainsi
 < \eta_{x_n, 1/n})
donc
, g(x_n)) < 1/n)
Bien sur, comme
 < \eta_{x_n, 1/n})
, a fortiori
 < 1/n)
-- Bilan --
Le
)
n'était pas explicité du tout !!
J'avais l'impression que
était une conséquence de
 < 1/n)
Merci pour tes encouragement !! En effet je prépare les oraux et typiquement si je bute sur ce genre de difficulté, à l'heure actuelle je serais très très ennuyé !!
Modifié en dernier par
chombier le 06 Juin 2018, 20:35, modifié 7 fois.
-
Elias
- Habitué(e)
- Messages: 369
- Enregistré le: 07 Fév 2016, 17:20
-
par Elias » 06 Juin 2018, 20:23
Voilà, c'est exactement ça.
Il faut s'habituer dans le Gourdon à ce que les raisonnements ne soient pas du tout détaillés
Mais c'est pas plus mal car ça fait réfléchir
Pseudo modifié : anciennement Trident2.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités
