DM - Théorème de Cantor-Bernstein
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 23 Oct 2013, 21:01
par Lostounet » 23 Oct 2013, 21:01
Bonsoir,
Je dois pour mon DM démontrer le théorème de Cantor-Bernstein. Le problème est que je ne comprends pas grand chose...
Soient E et F des ensembles. S'il existe une injection de E dans F et une injection de F dans , alors il existe une bijection de E sur F On va commencer par prouver un lemme:
1. Soient E un ensemble et
 \rightarrow P(E))
une application croissante (pour toutes parties A et B de E,
 \subset G(B))
)
Posons
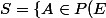 | A \subset G(A) \})
et

(a) Montrer que M appartient à S, en déduire que M est le plus grand élément de S.
Quelqu'un pourrait-il m'expliquer un peu cet exercice un peu abstrait pour quelqu'un qui vient de sortir de TS :hum:
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
eriadrim
- Membre Relatif
- Messages: 113
- Enregistré le: 19 Oct 2013, 12:04
-
 par eriadrim » 23 Oct 2013, 21:27
par eriadrim » 23 Oct 2013, 21:27
Bonsoir
Ici la notion de "plus grand" et "plus petit" est différente de celle rencontré dans

.

plus petit que

veut dire que
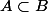
.
Ensuite pour la question, il faut montrer que

, c'est à dire que :
)
, ou encore :
)
A partir de la première partie de la question et la définition de "plus grand", tu devrais réussir à faire la deuxième partie :lol3:
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 23 Oct 2013, 23:44
par Sourire_banane » 23 Oct 2013, 23:44
C'est pas évident que M est dans S en tant que réunion de tout élément dans S ?
Puis si l'on essaye de prendre un élément Q de S dont M est partie, on s'aperçoit vite que Q ne peut être que M. Ou peut-être faut-il détailler un peu plus ?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 24 Oct 2013, 08:37
par arnaud32 » 24 Oct 2013, 08:37
Sourire_banane a écrit:C'est pas évident que M est dans S en tant que réunion de tout élément dans S ?
Puis si l'on essaye de prendre un élément Q de S dont M est partie, on s'aperçoit vite que Q ne peut être que M. Ou peut-être faut-il détailler un peu plus ?


d'apres toi M est dans S?
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 24 Oct 2013, 10:10
par Sourire_banane » 24 Oct 2013, 10:10
arnaud32 a écrit:

d'apres toi M est dans S?
Salut,
Dans ton exemple, il vaudrait mieux prendre n décrivant N*.
Et je pense bien que oui. Car ]0,1[ appartient bien à S, non ?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 24 Oct 2013, 10:25
par arnaud32 » 24 Oct 2013, 10:25
Sourire_banane a écrit:Salut,
Dans ton exemple, il vaudrait mieux prendre n décrivant N*.
Et je pense bien que oui. Car ]0,1[ appartient bien à S, non ?
oui tu as raison c'est N*
par contre je veux bien que tu me dises pour quel n tu as ]0,1[=]1/n; 1-1/n[
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 24 Oct 2013, 10:27
par Sourire_banane » 24 Oct 2013, 10:27
arnaud32 a écrit:oui tu as raison c'est N*
par contre je veux bien que tu me dise pour quel n tu as ]0,1[=]1/n; 1-1/n[
Pour n=1 ? :/ l'intervalle se réordonne automatiquement non ?
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 24 Oct 2013, 10:35
par beagle » 24 Oct 2013, 10:35
"Soient E et F des ensembles. S'il existe une injection de E dans F et une injection de F dans , alors il existe une bijection de E sur F "
l'injection de E dans F,
permet de définir deux sous-ensembles de F
l'ensemble G regroupe les éléments de F qui ont un antécédent
l'ensemble H regroupe les éléments de F qui n'ont pas d'antécédent
ensuite tu envoies de F vers E,
pour G la réciproque de l'injection E dans F, elle atteint tous les éléments de E.
pour H tu envoies dans E l'injection F dans E, elle atteint des éléments de E
Donc il y a surjection de F vers E
donc bijection
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 24 Oct 2013, 10:35
par arnaud32 » 24 Oct 2013, 10:35
]1;0[ c'est plutot vide
pour eviter une discution sterile sur ce point prenons:


-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 24 Oct 2013, 10:40
par Maxmau » 24 Oct 2013, 10:40
Lostounet a écrit:Bonsoir,
Je dois pour mon DM démontrer le théorème de Cantor-Bernstein. Le problème est que je ne comprends pas grand chose...
Soient E et F des ensembles. S'il existe une injection de E dans F et une injection de F dans , alors il existe une bijection de E sur F On va commencer par prouver un lemme:
1. Soient E un ensemble et
 \rightarrow P(E))
une application croissante (pour toutes parties A et B de E,
 \subset G(B))
)
Posons
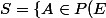 | A \subset G(A) \})
et

(a) Montrer que M appartient à S, en déduire que M est le plus grand élément de S.
Quelqu'un pourrait-il m'expliquer un peu cet exercice un peu abstrait pour quelqu'un qui vient de sortir de TS :hum:
Bonjour
la définition de S et la croissance de G impliquent : pour tout A de S , A contenu ds G(A) lui-même contenu dans G(M)
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 24 Oct 2013, 10:42
par arnaud32 » 24 Oct 2013, 10:42
beagle a écrit:"Soient E et F des ensembles. S'il existe une injection de E dans F et une injection de F dans , alors il existe une bijection de E sur F "
l'injection de E dans F,
permet de définir deux sous-ensembles de F
l'ensemble G regroupe les éléments de F qui ont un antécédent
l'ensemble H regroupe les éléments de F qui n'ont pas d'antécédent
ensuite tu envoies de F vers E,
pour G la réciproque de l'injection E dans F, elle atteint tous les éléments de E.
pour H tu envoies dans E l'injection F dans E, elle atteint des éléments de E
Donc il y a surjection de F vers E
donc bijection
en clair si F E->F injective et g F-> E injective
tu definis G=f(E) et H=compl(G)
tu definis une fonction h de F ->E par
h(y)=f^-1(y) si y est da G (ok car f est bijective de E sur G)
h(y)=g(y) si y est dans H (ok car g est definie sur F)
h est bien surjective car h(G)=E
mais h est elle injective?
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 24 Oct 2013, 10:43
par Sourire_banane » 24 Oct 2013, 10:43
arnaud32 a écrit:]1;0[ c'est plutot vide
pour eviter une discution sterile sur ce point prenons:


Quand tu as ]1,0[ l'ouvert ne se réarrange pas ?
Sinon ok, mais alors quel est l'argument qu'il faut utiliser ?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 24 Oct 2013, 10:52
par arnaud32 » 24 Oct 2013, 10:52
Sourire_banane a écrit:Quand tu as ]1,0[ l'ouvert ne se réarrange pas ?
Sinon ok, mais alors quel est l'argument qu'il faut utiliser ?
si tu prends comme definition de ]a,b[={x | x>a et xinf(a,b) et x3 ca evite toute confusion
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 24 Oct 2013, 10:55
par beagle » 24 Oct 2013, 10:55
arnaud32 a écrit:en clair si F E->F injective et g F-> E injective
tu definis G=f(E) et H=compl(G)
tu definis une fonction h de F ->E par
h(y)=f^-1(y) si y est da G (ok car f est bijective de E sur G)
h(y)=g(y) si y est dans H (ok car g est definie sur F)
h est bien surjective car h(G)=E
mais h est elle injective?
D'accord on part du principe que l'existence d'une injection f et d'une surjection g ne prouve pas l'existence d'une bijection possible h, parce qu'on ne le sait pas encore, c'est ça?Et qu'on le démontrera plus tard donc?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 24 Oct 2013, 11:00
par arnaud32 » 24 Oct 2013, 11:00
beagle a écrit:D'accord on part du principe que l'existence d'une injection f et d'une surjection g ne prouve pas l'existence d'une bijection possible h, parce qu'on ne le sait pas encore, c'est ça?Et qu'on le démontrera plus tard donc?
en fait ta construction de est mauvaise meme si l'idee est tres proche de la solution qui consite a faire ce que tu as fait mais non pas avec E comme partie de depart, mais une partie plus petite de E qui va permettre de rendre ta fonction h injective
http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Cantor-Bernstein
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 24 Oct 2013, 11:01
par Sourire_banane » 24 Oct 2013, 11:01
beagle a écrit:D'accord on part du principe que l'existence d'une injection f et d'une surjection g ne prouve pas l'existence d'une bijection possible h, parce qu'on ne le sait pas encore, c'est ça?Et qu'on le démontrera plus tard donc?
Arnaud a construit h telle que h(y)=f^(-1)(y) si y est dans G, donc comme f est bijective, f^(-1) aussi donc la restriction de f^(-1) à G est bien injective.
Si y est dans H, on a toujours H inclus dans F car H et G forment une partition de F. Alors g restreinte à H=h (si y est dans H) est injective par définition de g.
Donc h est bien injective.
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 24 Oct 2013, 11:09
par beagle » 24 Oct 2013, 11:09
arnaud32 a écrit:en fait ta construction de est mauvaise meme si l'idee est tres proche de la solution qui consite a faire ce que tu as fait mais non pas avec E comme partie de depart, mais une partie plus petite de E qui va permettre de rendre ta fonction h injective
http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Cantor-Bernstein
ma construction est gentille, je veux pas qu'on la dise mauvaise,
mais je ne savais pas trop à quoi vous jouyez ou jouillez, mème en français je suis pas bon, zut alors.
Je n'avais pas le droit de dire injection de f + surjection de g fait qu'il existe bijection h.
demande confirmation de ce que je n'avais pas le droit de faire.
je comprends ensuite ce que vous faites, ah oui c'est plus dur.
M'étonnait aussi qu'il faille faire l'exercice en binome Cantor et Bernstein.
je trouve que les groupes pour cet exo sont mal faits, on a mis deux bons ensembles!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 24 Oct 2013, 11:11
par arnaud32 » 24 Oct 2013, 11:11
Sourire_banane a écrit:Arnaud a construit h telle que h(y)=f^(-1)(y) si y est dans G, donc comme f est bijective, f^(-1) aussi donc la restriction de f^(-1) à G est bien injective.
Si y est dans H, on a toujours H inclus dans F car H et G forment une partition de F. Alors g restreinte à H=h (si y est dans H) est injective par définition de g.
Donc h est bien injective.
non h n'est pas injective, elle ne l'est que si H=vide
sinon tu prends y dans H h(y) est dans E et y'=f(h(y)) qui est dans G verifie h(y')=h(y)
or y et y' ne peuvent etre egaux par definition de G et H
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 24 Oct 2013, 11:26
par Sourire_banane » 24 Oct 2013, 11:26
arnaud32 a écrit:non h n'est pas injective, elle ne l'est que si H=vide
sinon tu prends y dans H h(y) est dans E et y'=f(h(y)) qui est dans G verifie h(y')=h(y)
or y et y' ne peuvent etre egaux par definition de G et H
Oulalah, bon, je vais me rendormir !
Et désolé pour l'embrouille

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 30 Oct 2013, 22:05
par Lostounet » 30 Oct 2013, 22:05
Re,
J'ai un peu de mal à justifier proprement que M est la partie maximale de S. C'est super intuitif...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
