Messieurs, mesdames, bonsoir.
Recemment j'ai revisite mes notions de geometrie de base, afin d'enseigner a de plus jeunes gens encore dans l'ignorance. Ce faisant, une particularite de la sphere et du cercle m'a frappe.
Pour la sphere, V = 4/3 Pi * r^3, Aext = 4 * Pi * r^2
Pour le cercle, A = pi * r^2, P = 2*Pi*r
J'ai revisite mon cours de calcul differentiel egalement, et je ne trouve pas la reponse :
Pourquoi est-ce que l'aire exterieure d une sphere est la derivee de son volume, et pourquoi est-ce que le perimetre d un cercle est la derivee de son Aire ? Autrement dit, Pourquoi dV/dr = Aext | dA/dr = P
Est-ce une pure coincidence ? est-ce que ca a a voir avec la symetrie de la sphere et du cercle ?
Notez qu avec le tetraedre, par exemple, ca ne marche pas (pour autant que j'aie reflechi), car il est difficile de restreindre d autres formes geometriques a un seul parametre seulement, hormis la sphere et le cercle, qui ne dependent que de r
Si quelqu'un veut bien me tirer de l'ignorance, je suis tout ouie ;)
Sur ce, mesdames, messieurs,
Bonne soiree
[PS] : Je sais que l'on peut prouver les formules de l'aire et du volume de la sphere en considerant
R = Sqrt[x^2 +y^2] {*}
et en la faisant pivoter autour de l axe Ox, on peut trouver l aire exterieure et le volume de cette sphere.. Cependant, le calcul requiert la connaissance de 2 Pi r, et de pi r^2, pour lesquels je ne sais pas demontrer, a l aide la fonction {*} que le perimetre = 2*pi*r.
Et toujours le meme probleme se pose, derivee entre les proprietes : coincidence, ou bon-sens?
Surface/Volume, Aire/Perimetre
2 messages
- Page 1 sur 1
Bonsoir,
Pour le cercle : la surface d'une couronne de rayon r et de largeur dr peut être approchée par :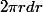 (dr petit devant r, on considère que la couronne est un rectangle allongé), ce qui donne comme surface du disque de rayon R
(dr petit devant r, on considère que la couronne est un rectangle allongé), ce qui donne comme surface du disque de rayon R 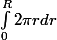 .
.
Pour la sphère le volume d'une couronne sphérique (ça ne doit pas être le bon nom mais je ne retrouve plus comment ça s'appelle) de rayon r et d'épaisseur dr est approximativement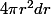 , d'où pour le volume
, d'où pour le volume 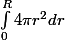 .
.
Avec un tétraèdre régulier on peut calculer le volume en le découpant horizontalement en triangles puis en intégrant de 0 à la hauteur, la dérivée du volume exprimé en fonction de la hauteur donne l'aire d'une face.
Pour le cercle : la surface d'une couronne de rayon r et de largeur dr peut être approchée par :
Pour la sphère le volume d'une couronne sphérique (ça ne doit pas être le bon nom mais je ne retrouve plus comment ça s'appelle) de rayon r et d'épaisseur dr est approximativement
Avec un tétraèdre régulier on peut calculer le volume en le découpant horizontalement en triangles puis en intégrant de 0 à la hauteur, la dérivée du volume exprimé en fonction de la hauteur donne l'aire d'une face.
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
