Suite de questions sur les complexes

[mydoudouitsk]

Bonjour, j'ai un exercice sur les complexes qui me pose problème vu mon niveau en math, pourriez vous m'aider?

voici l'énoncé:

déterminer les complexes z, tels que, z, 1/z et 1-z ont le même module.

j'ai passé z sous sa forme exponentielle afin d'extraire le module et ce dans chacun des cas, mais je trouve la même expression telle que

mais avec ça je ne vois pas comment je pourrais conclure, pourriez vous m'indiquer la bonne méthode?

[Nightmare]

Salut,

bon déjà, il faudrait mettre en équation l'énoncé.

On a deux égalités :

et (les deux combinées entraînant bien sûr que 1/z et 1-z ont aussi le même module, donc on a bien l'énoncé entier !)

La première équation peut aussi s'écrire soit ou encore dont l'ensemble des solution est évidemment le cercle unité.

il reste à trouver son intersection avec l'ensemble des points du plan dont l'affixe vérifie |z|=|1-z|. Peux-tu trouver cet ensemble et en déduire l'intersection?

[mydoudouitsk]

et bien si |z|=1 alors z peut s'écrire sous la forme z=exp(i\theta).
or |1-z|=1 donc 1-z=exp(i\theta)

puis-je réellement écrire que z=1-z et que donc z=1/2?

[Nightmare]

Non pas vraiment, mais indépendamment de la première équation, |z|=|1-z| décrit elle aussi un ensemble de point. Pour le trouver, tu peux par exemple poser z=x+iy

[mydoudouitsk]

Utiliser la forme algébrique? je sais pas si la prof sera ok vu qu'elle n'arrête pas de dire que c'était bon que pour la terminale! Merci pour le tuyau je tente avec cette forme!

[Nightmare]

On peut toujours raisonner géométriquement, si ta prof préfère :

Notons M(z) et M'(z-1). |z|=|z-1| se traduit par OM=OM' avec O origine du repère. En outre M et M' ont même partie imaginaire, donc même ordonnée dans le plan, et comme O est sur la médiatrice de [MM'], on en déduit que cette médiatrice n'est autre que l'axe des ordonnées. On en déduit que le milieu de M et M' est de partie réelle nulle, autrement dit Re(1/2(z+z-1))=0, soit Re(z)=1/2.

Réciproquement, on vérifie que tous les points sur la droite d'équation x=1/2 sont solutions.

[mydoudouitsk]

Soit z=a+ib
|1-z|²= (1-a)²+b²=|z|²=a²+b²
(1-a)²+b²=a²+b²
(1-a)²=a²
a=1/2

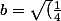|z|²=1 ... b²=1/4 donc ou

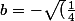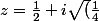donc ou

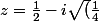[mydoudouitsk]

Ah ouais j'aime beaucoup l'explication géométrique! Merci beaucoup pour votre aide!
d'autres question me pose problème pourriez vous m'aider?

On me demande de résoudre
J'ai remplacé 1 par sin²x+cos²x mais ça ne donne rien, auriez vous une idée?