Structure algébrique d'un "pseudo"-idéal
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Viko
- Membre Relatif
- Messages: 209
- Enregistré le: 18 Juin 2017, 23:51
-
 par Viko » 18 Juil 2018, 20:29
par Viko » 18 Juil 2018, 20:29
Bonjour,
quelle(s) structure(s) algébrique peut-on mettre sur l'ensemble
:= \{P+Q | Q \in (P_0)\})
avec
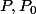
des polynômes à coefficients dans un corps et
)
l'idéal engendré par
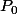
mise à part celle de sous espace-affine de
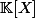
PS : ça n'a pas grand chose à voir mais sait-on exhiber des bases de
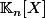
comportant n+1 vecteur et qui ne sont pas échelonnée en degrés ?
Qui ne maîtrise pas ses Cassinis, termine à Telecom Nancy

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 19 Juil 2018, 00:48
par Ben314 » 19 Juil 2018, 00:48
Salut,
Concernant la première question, c’est on ne peut plus vague : en fonction du contexte (i.e. de ce qu'on désire montrer), on peut munir cet ensemble de différentes structures, mais c'est vrai que, si l'on a pas besoin de la structure multiplicative de K[X] alors le premier truc qui vient à l'esprit, c'est la structure de sous espace affine.
Sinon, concernant la deuxième question, il y a bien sûr des tonnes de bases intéressantes de Kn[X] qui ne sont pas échelonnées en degrés. La première qui me vient à l'esprit, c'est évidement les polynômes servant de base aux polynôme d'interpolation de Lagrange, c'est çà dire les
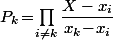
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités