Sous quel mesure peut-on affirmer"continue donc intégrable"?
4 messages
- Page 1 sur 1
Sous quel mesure peut-on affirmer"continue donc intégrable"?
Bonjour, peut on toujours dire qu'une fonction est intégrable car elle est continue ?
Re: Sous quel mesure peut-on affirmer"continue donc intégrab
Salut,
Sur un intervalle fermé borné (i.e. un segment), oui.
Sinon, non.
Sur un intervalle fermé borné (i.e. un segment), oui.
Sinon, non.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Sous quel mesure peut-on affirmer"continue donc intégrab
Salut,
La question manque cruellement de précision.
Sur quel espace mesurable te places-tu ? Pas trop quelconque, faut qu'il y ait une topologie pour parler de fonction continue.
Pour faire simple, la réponse est non et tu pouvais le deviner largement seul. En prenant par exemple la fonction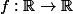 définie par
définie par  = 1) pour tout
pour tout  réel, elle est bien évidemment continue sur
réel, elle est bien évidemment continue sur  mais pas intégrable sur
mais pas intégrable sur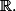
La question manque cruellement de précision.
Sur quel espace mesurable te places-tu ? Pas trop quelconque, faut qu'il y ait une topologie pour parler de fonction continue.
Pour faire simple, la réponse est non et tu pouvais le deviner largement seul. En prenant par exemple la fonction
Pseudo modifié : anciennement Trident2.
Re: Sous quel mesure peut-on affirmer"continue donc intégrab
Il y a les mesures à support compact qui peuvent t'aider.
En fait c'est le dual topologique, dual de l'ensemble des fonctions continues^*))
où X est un espace topologique
En fait c'est le dual topologique, dual de l'ensemble des fonctions continues
où X est un espace topologique
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
