Sous groupes Z/nZ

[math*]

bonjour j'aurai besoin d'aide pour un exo sur les structures algébriques. voici l'énoncé : soit n appartenant a N*. déterminer et dénombrer les sous groupes de (Z/nZ,+). merci de votre aide.

[ThSQ]

Y'a plein de façons de faire. Une marrante et pseudo-technique :

la proj canon

Si H est un ss-groupe de est un ss-groupe de Z contenu dans = un avé d|n.

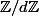
Réciproquement si d | n est un ss-groupe (à iso près) de

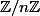
[math*]

merci de cette réponse. cependant il y a quelque chose que je ne comprend pas. pourquoi pi-1(Z/nZ)=nZ ?

[yos]

il y a quelque chose que je ne comprend pas. pourquoi pi-1(Z/nZ)=nZ ?

C'est plutôt Z.

[math*]

oui je suis bien daccord yos. mais que devient alors la solution au probleme? merci de votre aide.

[yos]

Ben est un ssg de Z donc un dZ et (et pas le contraire).

[math*]

oui daccord merci yos. jai bien compris.

[math*]

excuse moi yos mais en redigeant l'exercice je ne rends compte que je n'ai pas si bien compris que ça. on a donc si j'ai bien compris le début : dZ est un sous groupe de Z avec n|d. mais en fait je ne vois pas le rapport avec les sous groupes de Z/nZ. je me doute que c'est sûrement bête mais je crois qu'il ne manque un petit truc pour comprendre. merci d'avance pour quelques petites explications supplémentaires.

[math*]

Re bonsoir quelqu un pourrait il me fournir une explication ? merci et bonne soirée.

[yos]

Le reste correspond à ce que disait Thsq :
H ssg de Z/nZ,
ssg de Z,
,
en particulier contient c'est-à-dire nZ.
,
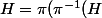car est surjectif.

[ThSQ]

Tiens en voulant corriger mon post j'ai dû le détruire tout à l'heure .... :marteau:

Remarquons que c'est pas spécifique de Z/nZ. Les sous-groupes de G/H sont les images par des sous-groupes de G qui contiennent H. Et ça se démontre pareil : et un sous-groupe de G et il contient