Bonjour
j'excuse d'avance si ce que je demande peu sembler anodin ou dans une section inappropriée
c'est parce que selon moi j'ai du mal à résoudre ce que je demande et que ça me semble plus dans un niveau de supérieur que celui du lycée
bon je me lance
la somme harmonique de 1/n = 1+1/2+1/3+...+n
j'aimerais savoir si on pouvait la récrire sous forme d'une suite avec un terme général en fonction de n et aussi s'il y avait une méthode particulière pour le faire
voila
merci pour les réponses
Somme et Terme General 2
12 messages
- Page 1 sur 1
muse a écrit:http://fr.wikipedia.org/wiki/S%C3%A9rie_(math%C3%A9matiques)
Vas dans exemples de references
merci pour le lien mais je n'ai pas très bien compris le o(1) je ne sais pas ce que c'est
Bonjour,
c un sujet tout à fait passionnant:
le terme principal de la série harmonique est ln(n)
cette différence) a pour limite
a pour limite  nombre appelé "constante d'Euler" que l'on conjecture transcendant.
nombre appelé "constante d'Euler" que l'on conjecture transcendant.
Ensuite, il y a des termes , dans le DL généralisé de- \gamma) , qui tendent vers zéro, que l'on doit pouvoir expliciter.
, qui tendent vers zéro, que l'on doit pouvoir expliciter.
rem: on sait que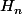 n'est pas un entier pour n>1.
n'est pas un entier pour n>1.
c un sujet tout à fait passionnant:
le terme principal de la série harmonique est ln(n)
cette différence
Ensuite, il y a des termes , dans le DL généralisé de
rem: on sait que
mathelot a écrit:Bonjour,
c un sujet tout à fait passionnant:
le terme principal de la série harmonique est ln(n)
cette différencea pour limite
nombre appelé "constante d'Euler" que l'on conjecture transcendant.
Ensuite, il y a des termes , dans le DL généralisé de, qui tendent vers zéro, que l'on doit pouvoir expliciter.
rem: on sait quen'est pas un entier pour n>1.
ça j'ai bien compris je te remercie
mais d'après moi le terme principal ln(n) ne correspond pas à une fraction à l'instant n donnée
c'est pour ça
d'après moi ça devrait ressembler à une fraction de puissance du style
a^n/b^n mais je ne sais pas comment la trouver
j'ajouterais que je m'excuse pour mes faibles compétences
elmouldi a écrit:d'après moi ça devrait ressembler à une fraction de puissance du style
a^n/b^n mais je ne sais pas comment la trouver
Pourquoi cela devrait-il se simplifier de cette façon? Tu crois que toutes les suites sont géométriques? Tu ne dois pas avoir fait beaucoup de maths pour avoir des exigences de cette sorte.
La quasi-égalité
yos a écrit:Pourquoi cela devrait-il se simplifier de cette façon? Tu crois que toutes les suites sont géométriques? Tu ne dois pas avoir fait beaucoup de maths pour avoir des exigences de cette sorte.
La quasi-égalitéest déjà miraculeuse.
je n'ai jamais dit que jetais fort en maths j'ai même repete de nombreuses fois a quel point jetais inculte
surtout aussi que je n'ai rien exigé du tout j'ai demandé si c'était faisable ou pas et s'il y avait une méthode
au passage j'ai emis la supposition que pour qu'on tombe sur des fractions dans des etapes il fallait aboutir a une expression de type fraction avec quelque chose en fonction de n (puissance, facteur, somme, ou une combinaison des 3)
donc comme j'ai dit plus haut, je viens ici sollicter une aide ou un conseil gentiment parce que j'ai plusieurs lacunes
elmouldi a écrit:surtout aussi que je n'ai rien exigé du tout j'ai demandé si c'était faisable ou pas et s'il y avait une méthode
Remplace "exigences" par "souhaits" dans mon précédent message.
elmouldi a écrit:au passage j'ai emis la supposition que pour qu'on tombe sur des fractions dans des etapes il fallait aboutir a une expression de type fraction avec quelque chose en fonction de n (puissance, facteur, somme, ou une combinaison des 3)
La propriété
Pour écrire ta somme plus simplement, il faudrait que chacun de ses termes soit la différence de deux termes consécutifs d'une autre suite
C'est l'analogue discret d'une recherche de primitive.
yos a écrit:Remplace "exigences" par "souhaits" dans mon précédent message.
La propriétééquivaut à celle-ci :
.
Pour écrire ta somme plus simplement, il faudrait que chacun de ses termes soit la différence de deux termes consécutifs d'une autre suite. Il y a des cas assez rares dans lesquels une telle suite
apparait naturellement : le cas des suites géométriques en est un. Le cas que tu donnes n'en est pas un.
C'est l'analogue discret d'une recherche de primitive.
j'ai très bien compris sauf la dernière phrase
par primitive tu veux dire élémentaire (ou de base) ou intégration.
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
