[théorème d'intégration terme à terme] écriture d'une intégr

[Supernova]

\Salut à vous!

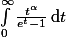
Tout est dit dans le titre, voilà mon intégrale où \alpha[/TEX] est un complexe tq
j'ai fais ça:

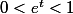
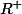
car et puis j'ai posé est intégrable sur pour tout mais j'ai pas su comment calculer l'intégrale de la valeur absolue de pour montrer qu'elle est convergente et appliquer le théorème ci-haut.

Can you help me?

Merci

[jlb]

[quote="Supernova"]\Salut à vous!

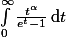
Tout est dit dans le titre, voilà mon intégrale où \alpha[/TEX] est un complexe tq
j'ai fais ça:

car [TEX]0 t^Re(alpha)*exp(-n/2)t) pour obtenir un majorant

puis intègre le tout pour faire apparaître le terme d'une série de Riemann ( Re(alpha) + 1) convergente.

[adrien69]

Salut !
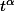
Regarde bien ton , tu ne trouves pas que le n'a pas vraiment de poids ?

Tu n'aurais pas envie (moi j'ai vraiment envie) de faire comme s'il n'existait pas ?

On peut -presque- le faire disparaître, tu vois comment ?

[Supernova]

En fait j'ai trouvé que c'est égal à

@Adrien: j'ai rien pigé de ce que tu as dis