Somme directe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 24 Jan 2015, 19:16
par capitaine nuggets » 24 Jan 2015, 19:16
Bonsoir,
L'ensemble des fonctions

dans lui-même peut-il s'écrire comme somme directe des fonctions paires de

dans lui-même et des fonctions paires de

dans lui-même ?
En d'autres termes, a-t-on :
[CENTER]
 = \mathcal{P(\mathbb{C}) \oplus \mathcal{I(\mathbb{C}))
[/CENTER]
où :
 = \{ f \mid f : \mathbb{C}\to \mathbb{C} \})
 = \{ f \in \mathcal{F}(\mathbb{C}) \mid f\ {\rm paire} \})
 = \{ f \in \mathcal{F}(\mathbb{C}) \mid f\ {\rm impaire} \})
A supposer que les termes "pair" et "impair" désignent la même chose que dans pour des fonctions de

dans lui-même.
Merci d'avance :+++:
-
lionel52
- Membre Relatif
- Messages: 274
- Enregistré le: 21 Nov 2012, 22:39
-
 par lionel52 » 24 Jan 2015, 19:24
par lionel52 » 24 Jan 2015, 19:24
Oui oui la démo est très générale et la décomposition est la même ue dans R : (f(z)+f(-z))/2 + (f(z)-f(-z))/2

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 24 Jan 2015, 19:38
par capitaine nuggets » 24 Jan 2015, 19:38
lionel52 a écrit:Oui oui la démo est très générale et la décomposition est la même ue dans R : (f(z)+f(-z))/2 + (f(z)-f(-z))/2
Ok merci pour la confirmation :++:
Oui, la décomposition est facile à obtenir (je trouve) grâce à
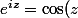+i \sin(z))
: elles sont données dans les formules d'Euler :+++:

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 24 Jan 2015, 20:37
par zygomatique » 24 Jan 2015, 20:37
capitaine nuggets a écrit:Oui, la décomposition est facile à obtenir (je trouve) grâce à
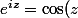+i \sin(z))
: elles sont données dans les formules d'Euler :+++:
:hein: :hein: :hein: :hein: :hein: :hein: :hein: :hein:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités