Somme et dérivée

[Sheyenne]

Bonjour,

J'aurais besoin d'aide pour un petit rafraîchissement de mémoire, je ne sais plus comment on calcul ce genre de somme : Sigma k2^(k-1)

Je sais que k2^(k-1) est la dérivée de 2^k, mais je ne me rappelle plus de la méthode à suivre

Merci d'avance à ceux qui pourront m'aider !

[capitaine nuggets]

Salut !

Pour , tu as . Donc en dérivant tu as

[LB2]

Bonjour,

méthode : calculer pour quelconque (en remarquant que c'est une dérivée), puis faire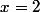

C'est la même idée que capitaine nuggets!

[fatal_error]

bj,

les souvenirs sont loin, mais pour intervertir dérivée et somme ne devrait-il pas y avoir convergence uniforme? (idem |x|<1)
(j'ai supposé que la somme était infinie...vu que pas de bornes)

[Sheyenne]

Merci pour vos aides j'ai réussi !

[capitaine nuggets]

Autre méthode :

.

[LB2]

bj,

les souvenirs sont loin, mais pour intervertir dérivée et somme ne devrait-il pas y avoir convergence uniforme? (idem |x|<1)
(j'ai supposé que la somme était infinie...vu que pas de bornes)

Il s'agit ici d'une somme finie, donc aucun problème de convergence.

Pour une somme infinie, on considère la série entière Elle est de rayon de convergence 1, en particulier, pour tout r < 1, on a convergence uniforme de la série sur l'intervalle [0,r]