Solution d'équation différentielle du second ordre.

[Jonny]

Bonjour,
je poste ici, mais le sujet est à cheval sur les maths et la physique (des maths dans la physique en fait :p)

Je sais résoudre une équa diff du second ordre avec équation caractéristique, recherche de la solution de l'équation homogène, puis d'une solution particulière. Ca c'est le schéma de base version maths.

Mon soucis se pose sur la résolution en physique. Ma prof devant une équation nous sort à chaque fois directement "la solution est du type ...", puis elle identifie.

Et en effet quand je résous avec ma méthode longue et fastidieuse, les résultats sont les mêmes.
Je me doute qu'elle ne résout pas instantanément (si ? Oo), mais qu'elle connaît les résultats de forme par coeur.
Comme ça a l'air bien pratique, j'aimerais les connaître aussi, mais tous les cours que je trouve sur le net me fournissent les mêmes méthodes que celles vues en maths.

Avez-vous une méthode pour identifer d'un coup d'oeil les formes de solutions ?

Merci d'avance.

[XENSECP]

Mdr ^^
Si tu avais un exemple ce serait mieux :)

[Jonny]

Justement, l'exemple qui m'a conduit à poster :

L'équation :

Je résous :
(Ec) :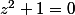
Deux racines complexes :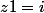 et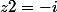

Donc ma solution d'équation homogène est :
qu'on peut encore écrire si je ne me trompe pas.

Une solution particulière évidente :

Donc solutions :

C'était pas très long pour celle là (surtout que la solution particulière est évidente), mais ma prof nous a sorti la solution directement, et elle fait ça à chaque fois.
Soit elle connait tout vraiment par coeur, soit elle voit quelque chose d'un coup d'oeil.

Par exemple, dans la solution homogène :

Avec alpha et beta les parties réelles et imaginaires de mes solutions d'équation caractéristique,
comment peut-on savoir sans poser (Ec) que alpha=0 et Beta=1 ?

Encore, là c'est assez vite vu, mais dès fois, c'est carrément impossible sans passer par le discriminant.

Si c'est juste du par coeur, tant pis, mais si il y a une méthode pratique rapide, j'aimerais la connaître

[XENSECP]

Mdr oui l'équation d'un oscillateur harmonique c'est super classique... je le fais de tête aussi ;)

D'ailleurs il reste la constante v dans le cos (pour répondre à ta pseudo-question sur les alpha et bêta)

[fourize]

bonjour;

celui la,comme beaucoup d'autre d'ailleurs, on est bien d'accord qu'il est faisable de tête. mais je pense aussi que ta prof vous donnes les exercices qu'elle enseigne depuis longtemps. du coup elle se rappelle des solutions .

mais je doute aussi qu'elle ferait jamais des trucs pour impressionner non plus avant tout c'est elle la prof :doh: et si tu la posais elle même la question???

[Jonny]

Non, c'est certain qu'elle ne fait pas ça pour impressionner, mais sûrement pour gagner du temps (je comprends qu'on va pas tout refaire à chaque fois).

Mais c'était tellement automatique que je me demandais si il n'y avait pas une astuce quand même ^^
Apparemment non, donc je vais attendre d'avoir imprimé tout ça avant de pouvoir recracher d'un coup.

Merci à vous.

[XENSECP]

Mdr il y a pas d'astuce...c'est juste super classique et vous êtes censé aller aussi vite... Tu raisonnes trop en termes de maths et pas assez en termes de physique... tu seras matheux et pas physicien quoi ^^

Les matheux ils font tout le blabla (ou les physiciens qui ont envie de s'amuser/ qui se font chier), les physiciens ils veulent le résultat pour interpréter, le calcul n'est pas la finalité du physicien...

Alala... rien à apprendre par coeur en tout cas... juste avoir compris :)

[busard_des_roseaux]

bjr,

si le second membre est une somme :


on cherche une solution particulière pour chaque équation:



et on ajoute les solutions particulières

si le second membre est on cherche une solution particulière sous la forme
sauf si 2 est racine de l'équation caractéristique, dans ce cas
on cherche une solution particluière sous la forme

si le second membre est de la forme cos(3x)
on cherche une solution particulière sous la forme Acos(3x)+Bsin(3x)
sauf si 3i est racine de l'équation caractéristique
auqel cas on cherche sous la forme


dans le cas général, je ne me rappelle plus trop
si l'on peut faire varier les deux constantes et chercher une solution
particulière sous la forme

de plus, en général, les déterminants des systèmes
à résoudre pour trouver des solutions particulières vérifient une équation
différentielle du type

et s'ils ne s'annulent pas en un point, ne s'annulent jamais,
ce qui permet de résoudre le système de Cramer.