Signature forme quadratique

[deliche]

BOnjour j'aimerai bien savoir comment faire pour trouver la signature d'une forme quadratique par exemple q((x,y))=

Code: Tout sélectionner

x^2-y^2

est-ce que c'est direct ou il faut faire une reduction de gauss?

[pascal16]

Je n'ai jamais fait de signature de formes quadratiques, mais
Si ta base a que 2 vecteurs dont l'un a une image toujours positive et l'autre toujours négative, ça ne fait pas une signature égale à (1;1) ?

[Ben314]

Salut,

Si ta base a que 2 vecteurs dont l'un a une image toujours positive et l'autre toujours négative, ça ne fait pas une signature égale à (1;1) ?

Non, ça ne suffit pas de regarder les signes des images des éléments de la base : par exemple si q(x,y)=x²+y²+lambda.xy alors les élément de la base ont tout les deux des images égale à +1 alors que la signature dépend de lambda.

Sinon, @deliche, pourrait tu te fendre d'une petite explication concernant la façon dont tu fait une "réduction de Gauss" dans le cas présent ?

P.S. Attention aussi (pour les "répondant" que la notion de "signature", tout le monde le note pas exactement de la même façon : la tendance est plutôt "nombre de >0 ; nombre de <0" avec des parenthèses, mais il y a encore des bouquins où on emploie une (voire des) autre façon de donner (la même) réponse, par exemple en mettant un troisième terme correspondant à "nombre de 0" histoire que la dimension se retrouve à travers la signature.
Bref, concernant ce qu'est (du verbe être) la signature, tout le monde est d'accord, par contre concernant la façon dont on l'écrit, c'est pas complètement standard.

[deliche]

Moi j'ai pas l'impression qu'on puisse faire une reducion de Gauss vu que les deux termes sont carré.

[Ben314]

Oui, (et ça serait mieux que ce soit "plus qu'une impression") :
Le but d'une "réduction de gauss", c'est d'écrire une forme quadratique sous forme de somme/différence de carrés.
Or, ici, ben dès le départ c'est déjà sous cette forme là donc y'a rien à "réduire" et juste à "lire".

Et ce que tu "lit", c'est qu'il y a un "+" et un "-" et c'est ça la "signature".
A toi de regarder dans ton cours comment ton prof./bouquin l'écrit ce "1 + et 1 -" : il y a de forte chance que ce soit (1,1), mais c'est pas sûr et certain (mais de toute façon, lorsque tu aura en t'en servir sous une forme ou une autre, il faudra évidement que ce que le truc dit, c'est "un + et un -" donc la notation n'a pas grande importance)

[deliche]

J'ai une derniere question je dois determiner l'ensemble des ses vecteurs isotropes mais je ne sais pas trop comment faire. En tout cas commencer.

[Ben314]

En tout cas commencer.

Ben... exactement comme dans 95% des exercices "de bases" (i.e. ceux qu'on fait en premier sur une notion donnée) : écrire la définition du bidule.

En général, le "cône isotrope", c'est l'ensemble des vecteur V de E tels que q(V)=0.
Donc ici c'est l'ensemble des (x,y) dans R² tels que q(x,y)=0 c'est à dire x²-y²=0.

[deliche]

Donc on a q(u)=0 <=> x=0 et y=0 donc on aurait u=(0,0) avec u=(x,y) ?

[Ben314]

Perso, ça m'étonnerais plus que beaucoup que la seule et unique solution de l'équation x²-y²=0 soit x=y=0...
Y'en a pas au moins une autre (voire des tas d'autres) qui te "sautent aux yeux" ?

[deliche]

Comme on a x^2-y^2=0 on a x^2=y^2 donc x=y ou x=-y donc u=(x,x) ou u=(x,-x)

[Ben314]

Oui, c'est mieux.
Donc le cône isotrope, c'est la réunion de deux droites vectorielles.

[deliche]

Donc l'ensemble des vecteur isotropes c'est (0,0). Je pose {uE | q(u)=0}={x | (x,x)=0 et (x,-x)=0}={x | x=0}
Je sais pas si je peut le formuler comme ca

[Ben314]

Donc l'ensemble des vecteur isotropes c'est (0,0). Je pose {uE | q(u)=0}={x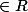 | (x,x)=0 et (x,-x)=0}={x 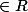| x=0}
Je sais pas si je peut le formuler comme ca

Non, surement pas, c'est sans queue ni tête quasiment du début à la fin.
- Déjà, l'ensemble des vecteurs isotrope, ç'est surement pas (0,0) vu que (0,0), c'est pas un ensemble.
- A la rigueur, ça pourrait être l'ensemble contenant l'unique vecteur (0,0) de R², c'est à dire l'ensemble {(0,0)}, mais c'est en contradiction complète avec le calcul que tu vient de faire qui montre justement que le cône isotrope, il contient des tonne de vecteurs autre que (0,0).
- Ensuite, quand on commence un phrase par "je pose", ben ce qui est attendu derrière, c'est qu'on définisse quelque chose. Du style "je pose a=5" ou bien "je pose Delta=b²-4ac" ou "je pose Un=3n+5 pour tout entier n".
Là tu "pose" rien du tout vu qu'il y a tu défini rien ensuite. Et en plus, vu la question, je vois pas bien ce que tu as à définir (donc à poser).
- Ensuite, un truc du style {uE t.q. . . . } = {x t.q. . . .} c'est forcément du grand n'importe quoi : un ensemble d'éléments de E, ça risque pas d'être égal à un ensemble de réels (à moins que E=R, mais ce n'est évidement pas le cas.
- Et ça : (x,x)=0 et (x,-x)=0, toujours aussi saugrenu : comment veut tu qu'un couple (quelconque) soit égal à un réel !!! Est ce que ça te viendrait à l'esprit dans la vie courante de dire que la voiture de ton voisin, c'est le canard de ta sœur ? Une voiture, quelle qu'elle soit, ça peut pas être égal à un canard, quel qu'il soit et là ben c'est exactement pareil, un couple ça peut pas être égal à un réel.
- Enfin ça : {x | x=0} exceptionnellement, ça a du sens, mais c'est complètement couillon : l'ensemble des réels qui sont égaux à 0, ben c'est l'ensemble {0} et je vois pas l'intérêt de l'écrire autrement que comme ça.
De nouveau, c'est comme si en Français tu disait "l'ensemble des personnes qui s'appellent Pierre Durand et qui habitent 22 rue des lilas à Tourcoing" c'est certes pas "faux" comme formulation, mais ça fait on ne peut plus con, non ?

Bref, ce qu'il faut écrire c'est :
- Le cône isotrope c'est la réunion des deux droites vectorielles d'équation respectives y=x et y=-x.
Ou bien
- Le cône isotrope c'est la réunion des deux droites vectorielles engendrées respectivement par (1,1) et (1,-1).
Ou bien
- Le cône isotrope c'est Vect{(1,1)}Vect{(1,-1)}
Ou bien
- Le cône isotrope c'est l'ensemble des vecteurs de la forme (x,x) ou bien (x,-x) avec x réel quelconque.
Ou bien
- Le cône isotrope c'est {(x,x) | R} {(x,-x) | R}
Ou bien
- Le cône isotrope c'est l'ensemble des vecteurs (x,y) tels que y=x ou bien y=-x.
Ou bien
- Le cône isotrope c'est {(x,y)R² tels que y=x ou bien y=-x}
etc etc etc

Enfin, bref, y'a 36 000 façon de décrire le truc, du "pur français" au "pur symbolique", mais il faut évidement que ça ait du sens !!!!!!