Rotation de fonction
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 06 Juil 2009, 15:15
par Maks » 06 Juil 2009, 15:15
On va trouver.
Bon, déjà, fixons nous le cylindre. On le prend de rayon

, et d'axe

.
Il est déjà clair qu'on doit avoir
^2+z(t)^2=R^2)
.
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 06 Juil 2009, 15:19
par sky-mars » 06 Juil 2009, 15:19
donc paramétrisation du cylindre
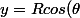, \theta \in [0;2\pi]\\ <br />z= R sin(\theta)\\<br />x= a , a \in R)
-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 06 Juil 2009, 15:22
par Maks » 06 Juil 2009, 15:22
Et si on disait simplement y(t)=f(t).
De manière qu'on aurait en fait :
=t \\<br />y(t)=f(t) \\<br />z(t)= \sqrt{R^2-f(t)^2})
Non ?
J'ai l'impression que ça marche.
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 06 Juil 2009, 15:25
par sky-mars » 06 Juil 2009, 15:25
ici f c'est la fonction sinus sans être incliné ou bien incliné ?
-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 06 Juil 2009, 15:26
par Maks » 06 Juil 2009, 15:26

est quelconque, mais donnée sous forme cartésienne, malheureusement. Il faut trouver autre chose pour le sinus tourné.
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 06 Juil 2009, 15:28
par sky-mars » 06 Juil 2009, 15:28
c'est une fonction qui axé par rapport à l'axe x mais si on souhaite tenir en compte le paramètre d'inclinaison ?
-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 06 Juil 2009, 15:29
par Maks » 06 Juil 2009, 15:29
J'y réfléchis.
-
Zavonen
- Membre Relatif
- Messages: 213
- Enregistré le: 23 Nov 2006, 10:32
-
 par Zavonen » 06 Juil 2009, 15:30
par Zavonen » 06 Juil 2009, 15:30
l'application :
(x,y) --->
,sin(y2\pi /h),x/L))
constitue une représentation conforme du rectangle de largeur L, de hauteur h dont le coin inférieur gauche est à l'origine sur le cylindre de rayon 1 et de hauteur 1.
Si vous avez une fonction y=f(x) tracée dans ce rectangle, la courbe paramétrée sur ce cylindre sera:
x--->
2\pi /h),sin(f(x)2\pi /h),x/L))
Si vous la voulez sur un cylindre de hauteur H et de rayon R
x--->
2\pi /h),Rsin(f(x)2\pi /h),Hx/L))
Si la courbe est tracée dans un autre rectangle, faites une simple translation de ce rectangle pour l'amener sur le précédent.
-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 06 Juil 2009, 15:32
par Maks » 06 Juil 2009, 15:32
Merci pour cette réponse Zavonen. Nous avions déjà réussi à "plaquer" une fonction du type y=f(x) sur un cylindre, mais malheureusement, la fonction que souhaite plaquer sky-mars n'est pas donnée de cette manière !
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 06 Juil 2009, 15:38
par sky-mars » 06 Juil 2009, 15:38
et pourquoi on essaierai pas de paramétrer les hélices pour un motif donnée ?
-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 06 Juil 2009, 15:38
par Maks » 06 Juil 2009, 15:38
C'est-à-dire ?
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 06 Juil 2009, 15:41
par sky-mars » 06 Juil 2009, 15:41
le sinus collé sur un cylindre sa serai une hélice, on pourrait définir le pas de l'hélice par rapport à la périodicité de ce sinus ou quelque chose dans le genre :marteau: :marteau: :marteau:
-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 06 Juil 2009, 15:47
par Maks » 06 Juil 2009, 15:47
Oui mais au final, tu veux une courbe du genre
=... \\<br />y(t)=... \<br />z(t)=... \\)
Non ?
-
Zavonen
- Membre Relatif
- Messages: 213
- Enregistré le: 23 Nov 2006, 10:32
-
 par Zavonen » 06 Juil 2009, 15:53
par Zavonen » 06 Juil 2009, 15:53
Maks a écrit:Merci pour cette réponse Zavonen. Nous avions déjà réussi à "plaquer" une fonction du type y=f(x) sur un cylindre, mais malheureusement, la fonction que souhaite plaquer sky-mars n'est pas donnée de cette manière !
Si elle est donnée sous forme de courbe paramétrée cela ne change absolument rien, il suffit de remplacer x et y par x(t) et y(t) dans la représentation.
-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 06 Juil 2009, 16:00
par Maks » 06 Juil 2009, 16:00
Alors je n'ai pas compris ta méthode. Au final, que proposes-tu comme équation pour répondre à la question de sky-mars ? Lui a une courbe parametrée du type (x(t),y(t)).
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 06 Juil 2009, 16:05
par sky-mars » 06 Juil 2009, 16:05
Pour moi , il est serai plus pratique d'avoir une courbe paramétrée
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 06 Juil 2009, 16:13
par sky-mars » 06 Juil 2009, 16:13
Zavonen a écrit:l'application :
(x,y) --->
,sin(y2\pi /h),x/L))
constitue une représentation conforme du rectangle de largeur L, de hauteur h dont le coin inférieur gauche est à l'origine sur le cylindre de rayon 1 et de hauteur 1.
Si vous avez une fonction y=f(x) tracée dans ce rectangle, la courbe paramétrée sur ce cylindre sera:
x--->
2\pi /h),sin(f(x)2\pi /h),x/L))
Si vous la voulez sur un cylindre de hauteur H et de rayon R
x--->
2\pi /h),Rsin(f(x)2\pi /h),Hx/L))
Si la courbe est tracée dans un autre rectangle, faites une simple translation de ce rectangle pour l'amener sur le précédent.
donc pour mon cas sa serai le cylindre de hauteur H et de rayon r.
quand tu parle de representation conforme ( c'est en rapport avec les transformation conforme comme en analyse complexe?)
-
Zavonen
- Membre Relatif
- Messages: 213
- Enregistré le: 23 Nov 2006, 10:32
-
 par Zavonen » 06 Juil 2009, 16:24
par Zavonen » 06 Juil 2009, 16:24
 ---> ( cos(y2\pi /h),sin(y2\pi /h),x/L))
Et bien dans le cas d'une courbe paramétrée t -->(x(t),y(t))
située dans le rectangle que j'ai indiqué
Elle deviendrait sur le cylindre:
2\pi /h),Rsin(y(t)2\pi /h),Hx(t)/L))
Sinon il faut décaler.
-
Zavonen
- Membre Relatif
- Messages: 213
- Enregistré le: 23 Nov 2006, 10:32
-
 par Zavonen » 06 Juil 2009, 16:28
par Zavonen » 06 Juil 2009, 16:28
quand tu parle de representation conforme
conserve les angles.
NB: Je n'en suis pas (plus) absolument sûr, mais cette condition n'est peut-être pas absolument nécessaire.
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 06 Juil 2009, 17:20
par sky-mars » 06 Juil 2009, 17:20
je comprends pas trop ta representaiton conforme , pourquoi un rectangle ??
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités