Rotation de fonction
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 06 Juil 2009, 13:37
par sky-mars » 06 Juil 2009, 13:37
Bonjour
Je souhaiterai déterminer l'équation d'une fonction ayant subit une rotation d'angle

et de centre

Soit f une fonction périodique et g étant la rotation de f.
Merci
-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 06 Juil 2009, 13:46
par Maks » 06 Juil 2009, 13:46
Bonjour.
C'est quoi une rotation de fonction ?
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 06 Juil 2009, 13:50
par sky-mars » 06 Juil 2009, 13:50
je sais pas si je me réponds mais j'ai pensé à ca
si par exemple j'ai
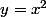
 )= M ( x; x^2))
M' image de M par r de centre O et d'angle

sa nous donnerai
; x^2 sin(\theta) ))
non ?
et ma fonction serait :
) = x^2 sin (\theta))
? on serait obligé de le tracer sur excel alors ?
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 06 Juil 2009, 13:51
par sky-mars » 06 Juil 2009, 13:51
je sais pas si j'arrive à être clair dans ce que je dit désolé
Par exemple j'ai sinus ! et je voudrai l'incliné de 20° et je souhaiterai déterminé son équation
-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 06 Juil 2009, 13:52
par Maks » 06 Juil 2009, 13:52
Ah, tu veux en fait effectuer une rotation sur le GRAPHE de la fonction, donc.
En effet, un paramétrage réalise facilement cette opération.
-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 06 Juil 2009, 13:56
par Maks » 06 Juil 2009, 13:56
Dans certains cas il sera facile d'obtenir une équation du type
)
, mais dans d'autres cas, cela sera impossible. Regarde par exemple
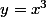
. Si tu la fais tourner un petit peu, tu n'a alors plus une fonction de x !
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 06 Juil 2009, 13:56
par sky-mars » 06 Juil 2009, 13:56
regarde cet exemple

j'ai généré un sinus simple puis j'ai fait une inclinaison et je souhaiterai avoir la fonction

-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 06 Juil 2009, 13:57
par Maks » 06 Juil 2009, 13:57
Ce n'est pas une fonction de

: à une abscisse correspondent plusieurs ordonnées.
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 06 Juil 2009, 14:00
par sky-mars » 06 Juil 2009, 14:00
okey donc la seule chose que je puisse faire c'est de paramétrer
Pour le sinus j'aurai
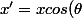)
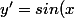 sin(\theta))
-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 06 Juil 2009, 14:09
par Maks » 06 Juil 2009, 14:09
Oui.
De manière plus générale, si tu veux tourner le graphe de la fonction f, d'un angle

autour de l'origine, il faut représenter le graphe de la fonction :
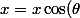 \\<br />y=f(x) \sin(\theta))
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 06 Juil 2009, 14:14
par sky-mars » 06 Juil 2009, 14:14
maintenant si par exemple je trace mes 4 sinus incliné comme sur la photo prédecente et je place tout ca sur un cylindre . J'obtiendrai les hélices, comme je fais pour obtenir sa paramétrisation ???
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 06 Juil 2009, 14:17
par sky-mars » 06 Juil 2009, 14:17
Comme ici par exemple :

ou

-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 06 Juil 2009, 14:46
par Maks » 06 Juil 2009, 14:46
C'est déjà plus ardu. Moi je dirai que la "courbe totale" est la réunion de courbes. Ca simplifierait les choses. Le problème se ramène donc à savoir comment mettre en équation un sinus collé sur un cylindre.
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 06 Juil 2009, 14:52
par sky-mars » 06 Juil 2009, 14:52
en effet sa revient à déterminer la paramétrisation d'un sinus collé sur un cylindre .... :cry: :doh: tu as une idée de comment trouver ça ?
-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 06 Juil 2009, 14:52
par Maks » 06 Juil 2009, 14:52
Je viens de me rendre compte que j'avais dit n'importe quoi pour la rotation de courbe !!
On trouve en fait :
=t \cos(\theta) - f(t) \sin(\theta) \\<br />y(t)=f(t) \cos(\theta) + t \sin(\theta))
(Passer par les complexes)
Mille excuses.
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 06 Juil 2009, 14:59
par sky-mars » 06 Juil 2009, 14:59
Comment as-tu trouvé ça ?
une rotation de centre O c'est pas :
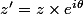
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 06 Juil 2009, 15:01
par sky-mars » 06 Juil 2009, 15:01
ah okey
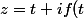)
et donc
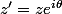
ok

d'ou ton résultat
-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 06 Juil 2009, 15:01
par Maks » 06 Juil 2009, 15:01
Si, et justement :
Si ton graphe est décrit par le point
 = (t,f(t)))
, son affixe est
)
, et donc
 e^{i\theta} = \left( t \cos(\theta) - f(t) \sin(\theta) \right) + i \left( f(t) \cos(\theta) +t \sin(\theta))
!
-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 06 Juil 2009, 15:02
par Maks » 06 Juil 2009, 15:02
Voilà !
Je suis en train de penser à ton sinus collé sur le cylindre.
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 06 Juil 2009, 15:13
par sky-mars » 06 Juil 2009, 15:13
le sinus collé sur le cylindre c'est balèze :S
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités